让我们回到《美诺篇》，苏格拉底指出美诺自己并不知道美德是什么并用奴隶显示是人都会自以为是。当然，苏格拉底首先承认自己也不知道美德是什么。美诺作为美德爱好者与宣传者，依然再次逼问苏格拉底“美德是否可教”这一不合逻辑的问题。《美诺篇》由此开始了引入形式逻辑的最简单的推理——假言推理。

这里要介绍有关Protagoras内容：

Protagoras 

(ca.490BC–420BC)

He was a pre-Socratic Greek philosopher and is numbered as one of the sophists by Plato.

In his dialogue Protagoras,Plato credits him with having invented the role of the professional sophist or teacher of virtue.

He is also believed to have created a major controversy during ancient times through his statement that man is the measure of all things.

This idea was very revolutionary for the time and contrasting  to other philosophical doctrines that claimed the universe was based on something objective, outside the human influence.

普罗泰格拉作为智者师傅（sophist，又译诡辩者：哲学和修辞学的教师），致力于道德和政治的联系。《美诺篇》中提到他做了40年的智者。普罗泰格拉的名言：人是万物的尺度，是存在者存在的尺度，也是不存在者不存在的尺度。

苏格拉底通过提问，迫使美诺自己得出：雅典没有一人能够教授美德，既然没有老师，没有学生，那么美德就是不可教的，因此推理出美德就不是知识。

                                                     If p, then q.Not q.Therefore,not p.

In classical logic, this is called modus tollens (or modus tollendo tollens, Latin for "the way that denies by denying“) ,one of the fundamental rules of inference.代数方程式就是这种推理的范例。

弗朗索瓦·韦达

弗朗索瓦·韦达（François Viète，1540－1603），1540年生于法国的普瓦图，1603年12月13日卒于巴黎。年轻时学习法律当过律师，后从事政治活动，当过议会的议员，在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究，第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂，带来了代数学理论研究的重大进步。

韦达在欧洲被尊称为“现代数学之父”。韦达最重要的贡献是对代数学的推进，他最早系统地引入代数符号，推进了方程论的发展。韦达用“分析”这个词来概括当时代数的内容和方法。他创设了大量的代数符号，用字母代替未知数，系统阐述并改良了三、四次方程的解法，指出了根与系数之间的关系。给出三次方程不可约情形的三角解法。著有《分析方法入门》、《论方程的识别与订正》等多部著作。

韦达从事数学研究只是出于爱好，然而他却完成了代数和三角学方面的巨著。他的《应用于三角形的数学定律》（1579年）是韦达最早的数学专著之一，可能是西欧第一部论述6种三角形函数解平面和球面三角形方法的系统著作。他被称为现代代数符号之父。韦达还专门写了一篇论文"截角术"，初步讨论了正弦（sin），余弦（cos），正切弦的一般公式，首次把代数变换应用到三角学中。他考虑含有倍角的方程，具体给出了将COS(nx)表示成COS(x)的函数并给出当n≤11等于任意正整数的倍角表达式了。

他的《解析方法入门》一书（1591年），集中了他以前在代数方面的大成，使代数学真正成为数学中的一个优秀分支。他对方程论的贡献是在《论方程的整理和修正》一书中提出了二次、三次和四次方程的解法。

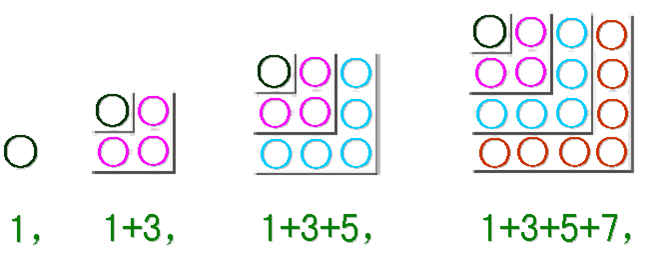
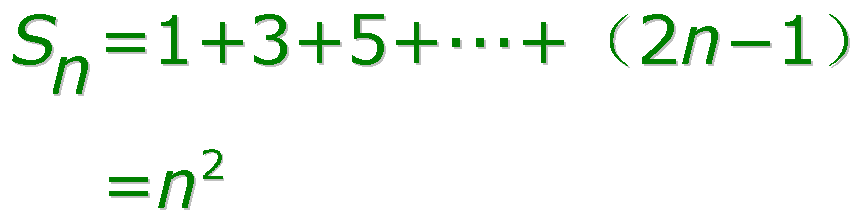
                                                     正方形数：奇数之和整数的平方。

Pythagoras派的“形数”的推导也是一种假言推理：假设和为某种几何图形。

Meno is again at a loss, and Socrates suggests that they have made a mistake in agreeing that knowledge is required for virtue. He point sout the similarities and differences between "right opinion" and "knowledge".We seem to find that the ideal of knowledge is irreconcilable with experience. In human life there is indeed the profession of knowledge of cause, but right opinion is our actual guide.

例如：太阳每天都从东方升起。这句话是知识吗？但是，“日出”只是地球动物从感觉经验得出的万年错觉，比如在月球上看见的是“地出”：

地球动物凭感觉经验得出的大多是有助于他/它们生存的“正确的见解”，也就是没有经过理性推理的约定俗成的东西。

Socrates said：Virtue comes by divine dispensation to those who have it. It’s not knowledge, it’s right opinion.

Socrates said：Right opinion isn’t stable，but knowledge is bound by the tie of cause.

因此，计算器如果设计与生产过程合格，它就代表了正确的意见，但是它不会推理，不能回答为什么？所以，它不能代表知识，当然更代表不了科学，它是无知的。同样道理，如果中小学满足于灌输，让学生疲于背诵或者重复训练，而无任何机会学习推理的方法，回答为什么这样的苏格拉底诘问，乘法口诀背的再熟也只能当个好的出纳，绝无成为科学家的可能。这就是百年以来我国中小学科学教育形成的痼疾，根子当然在于我国悠久的科举制度。

相关链接：

美国芝加哥大学数学学士，哈佛大学科学史博士，美国国家级数学名师Judith V. Grabiner教授的授课内容。

Prof. Grabiner said:Mathematics, in many ways, is like philosophy. This is not just because they both use logic.It's even more important to think that people in both fields care deeply about answering the question "why?"Proofs, whether in philosophy or in mathematics, answer the question "why" and takes us from right opinion to knowledge.