科学启蒙(Enlightenment of Science)

目录

  • 1 绪论
    • 1.1 易中天悖论
    • 1.2 钱学森问题
    • 1.3 科学是什么？
    • 1.4 爱因斯坦定义科学
    • 1.5 科学起源
    • 1.6 欧洲历史简介
    • 1.7 通识教育是什么？
    • 1.8 学习要点
  • 2 哲学、数学、科学同时起源于古希腊
    • 2.1 科学祖师在哪里？
    • 2.2 新月沃土
    • 2.3 地中海
    • 2.4 古希腊神话
    • 2.5 《神谱》与宇宙起源说
    • 2.6 理性之门
      • 2.6.1 盗用神权
      • 2.6.2 剥夺神权
      • 2.6.3 寻求普遍性
    • 2.7 理性之祖Thales
    • 2.8 原创何来？
  • 3 古希腊三杰建立形式逻辑体系
    • 3.1 古希腊哲学简介
    • 3.2 前苏格拉底哲学家中的其他科学家
    • 3.3 苏格拉底简介
    • 3.4 苏格拉底之问
    • 3.5 苏格拉底之法
    • 3.6 苏格拉底之死
    • 3.7 理性是什么？
    • 3.8 柏拉图简介
    • 3.9 柏拉图的“回忆”说
    • 3.10 柏拉图定义“意见”与“知识”
    • 3.11 柏拉图的“洞穴喻”
    • 3.12 柏拉图正多面体四原素说
    • 3.13 柏拉图的《理想国》
    • 3.14 柏拉图的理念、理型与共相
    • 3.15 理念是什么？
    • 3.16 柏拉图定义“哲学”
    • 3.17 柏拉图的“太阳隐喻”
    • 3.18 柏拉图的“线喻”
    • 3.19 理念、理型的词源
    • 3.20 亚里斯多德完成形式逻辑体系
  • 4 形式逻辑体系启蒙教科书
    • 4.1 跟谁学逻辑？
    • 4.2 欧几里德原本
    • 4.3 “自学”是扯淡
    • 4.4 欧几里德原本的内容
    • 4.5 欧几里德的“定义”
    • 4.6 欧几里德的“公设”
    • 4.7 欧几里德的“共识”
    • 4.8 欧几里德的“证明”
    • 4.9 古希腊科学是什么？
  • 5 从自然哲学到自然科学之路
    • 5.1 古希腊科学的创新亮点
    • 5.2 荒谬的亚里斯多德物理学
    • 5.3 阿基米德
    • 5.4 中世纪的阿拉伯科学
      • 5.4.1 西方的科学导师海什木
      • 5.4.2 西方的哲学、医学导师阿维森纳
    • 5.5 中世纪的西方科学
      • 5.5.1 罗吉尔•培根
      • 5.5.2 牛津大学校长罗伯特•格罗塞特
      • 5.5.3 冲力说理论
      • 5.5.4 巴黎大学校长让•布里丹
      • 5.5.5 牛津计算者与默顿匀加速运动定律
      • 5.5.6 尼古拉•奥里斯梅与运动的几何表示
      • 5.5.7 奥卡姆剃刀
    • 5.6 文艺复兴简介
    • 5.7 “通才”或者“文艺复兴人”
      • 5.7.1 达•芬奇
      • 5.7.2 文艺复兴式科学家盖姆
    • 5.8 天主教会的神职科学家
    • 5.9 科学革命简介
    • 5.10 科学革命英雄谱
      • 5.10.1 Andreas Vesalius 维萨留斯
      • 5.10.2 Christopher Clavius 克拉维
      • 5.10.3 Tycho Brahe 第谷•布拉赫
      • 5.10.4 William Gilbert 威廉•吉尔伯特
      • 5.10.5 Thomas Hobbes 托马斯•霍布斯
      • 5.10.6 Baruch Spinoza 斯宾诺莎
      • 5.10.7 Robert Boyle 罗伯特•波义耳
      • 5.10.8 Robert Hooke 罗伯特•胡克
      • 5.10.9 Christiaan Huygens 惠更斯
      • 5.10.10 Simon Stevin 力学先驱
      • 5.10.11 “科学革命”六人行
        • 5.10.11.1 哥白尼
        • 5.10.11.2 培根
        • 5.10.11.3 伽利略
        • 5.10.11.4 开普勒
        • 5.10.11.5 笛卡尔
        • 5.10.11.6 牛顿
  • 6 科学的基石：经验 + 理性
    • 6.1 科学界为何粉培根？
    • 6.2 培根的“四个偶像”
    • 6.3 科学探索的培根方法
    • 6.4 培根与英国经验主义传统
    • 6.5 归纳法的致命伤
    • 6.6 笛卡尔简介
    • 6.7 笛卡尔科学方法“四戒律”
    • 6.8 笛卡尔几何学
    • 6.9 笛卡尔几何PK欧几里德几何
    • 6.10 笛卡尔PK培根
  • 7 牛顿建立第一个科学体系
    • 7.1 伽利略开创现代科学
    • 7.2 伽利略的《论两种新科学》
    • 7.3 开普勒行星运动三定律
    • 7.4 牛顿简介
    • 7.5 牛顿的老师
    • 7.6 《自然哲学的数学原理》
    • 7.7 牛顿“发现”“定律”了吗？
    • 7.8 牛顿的光学
    • 7.9 牛顿的研究方法
    • 7.10 牛顿的影响无以伦比
  • 8 爱因斯坦、狄拉克开创现代科学体系
    • 8.1 李政道先生的启蒙老师讲牛顿
    • 8.2 动能概念的发明
    • 8.3 古典力学体系
    • 8.4 牛顿以来的基本物理学发现
    • 8.5 爱因斯坦简介
    • 8.6 相对论与量子力学
    • 8.7 现代科学体系
  • 9 科学的核心是科学方法
    • 9.1 科学方法总结
    • 9.2 量子物理学始创者所用科学方法举例
      • 9.2.1 普朗克的量子理论
      • 9.2.2 玻尔的量子理论
      • 9.2.3 德布罗意的量子理论
      • 9.2.4 海森堡的量子理论
      • 9.2.5 狄拉克的量子理论
      • 9.2.6 薛定谔的量子理论
    • 9.3 科学范式与科学革命中的范式转变
    • 9.4 科学是什么？
  • 10 它山之石，可以攻玉
    • 10.1 徐光启遗教：苟利于国，远近何论焉？
    • 10.2 “西学中源”实乃误国之妄言
    • 10.3 日本科学崛起之启示
    • 10.4 解决钱学森问题之法则
笛卡尔几何学


在几何任何问题，可以很容易地降低到这样的条款的某些直线的长度的知识足以应付其建设。

                                                                                                                                - 笛卡尔

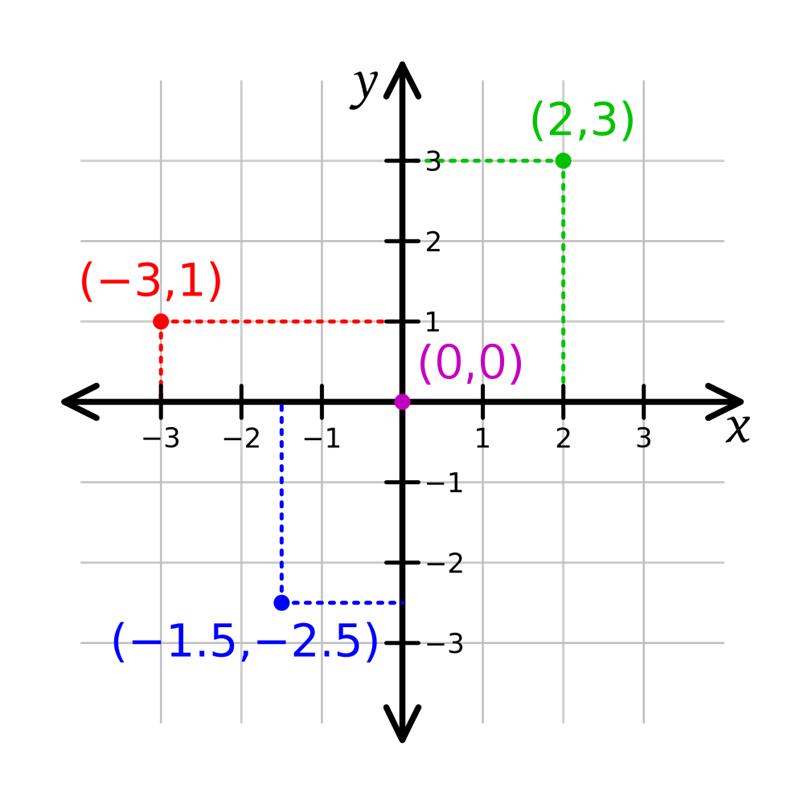
笛卡尔本人并没有作出坐标系，但他完全揭示了笛卡尔坐标系的根本特征。

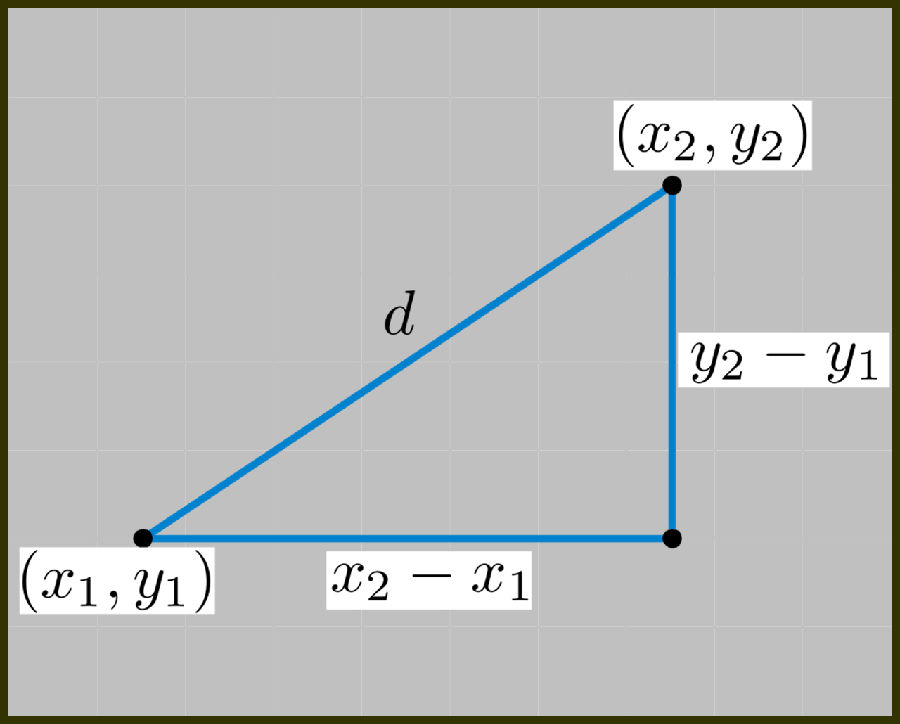
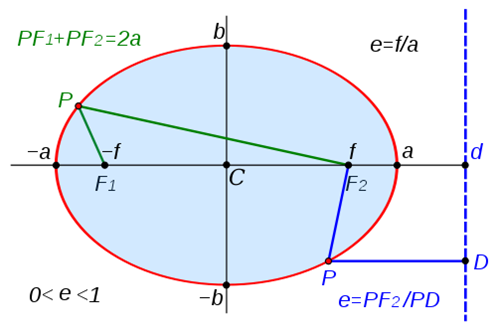
解析几何的根本：毕氏Theorem.The的Euclide和两点与笛卡尔坐标（X平面之间艾斯坦斯1， Ÿ 1）和（x 2， Ÿ 2）是

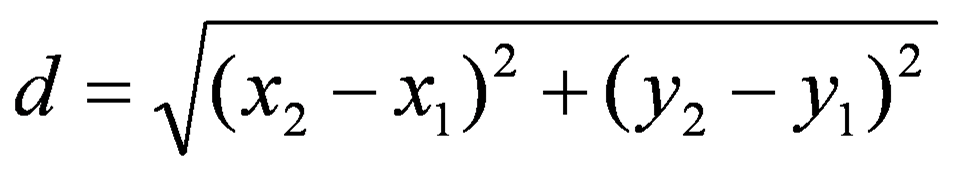
这是毕氏定理的笛卡尔版本。

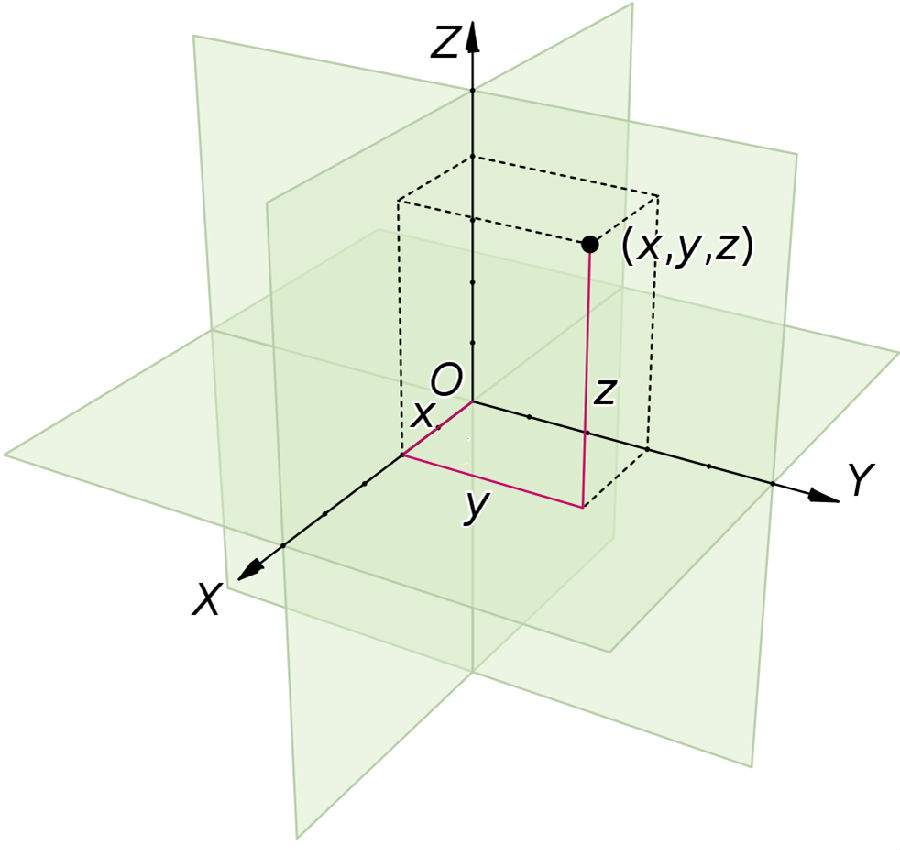
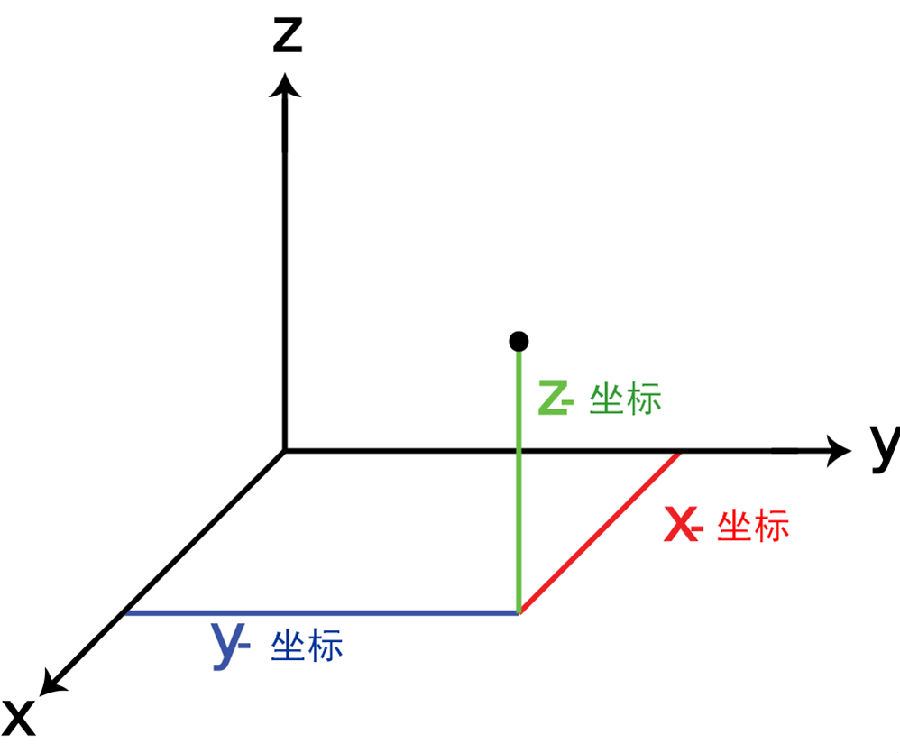
在三维空间中，点之间的距离（X 1， ý 1， Ž 1）和（x 2， ý 2， Ž 2）是

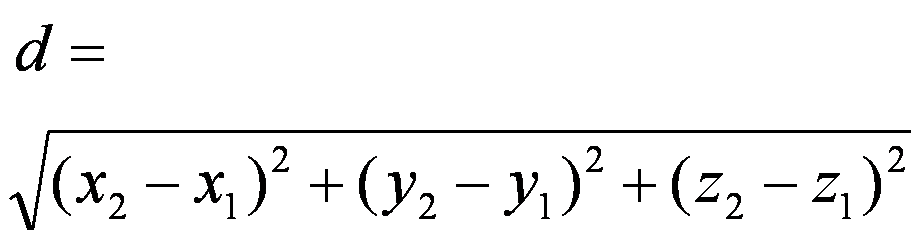
这可以通过毕氏定理的两个连续的应用程序来获得。

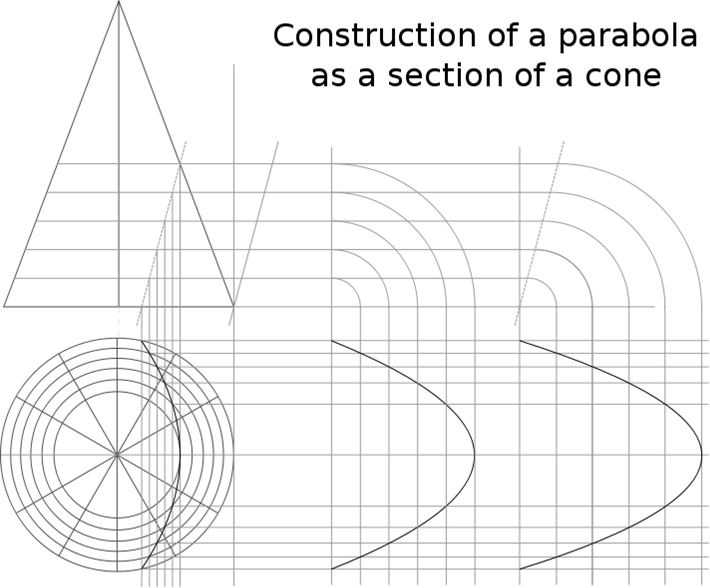
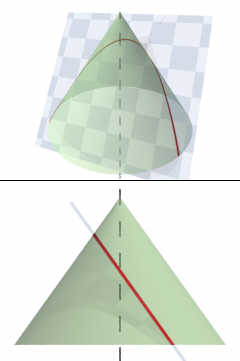抛物线（从希腊παραβολή）是圆锥部，右圆锥面的交点并平行于该表面的生成直线的平面。

关于圆锥曲线的已知最早的工作是由Menaechmus，谁被称为他与柏拉图的友谊。

 

抛物线罗盘由Leonardoda达·芬奇设计的。

从欧几里德到微分几何：

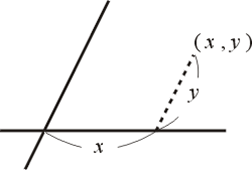
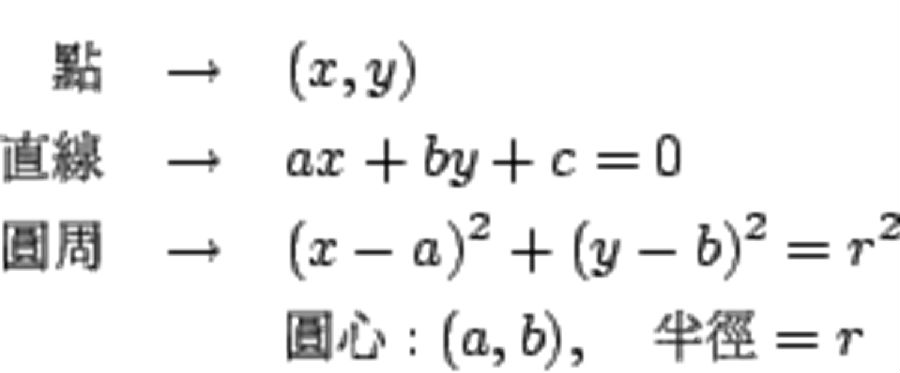
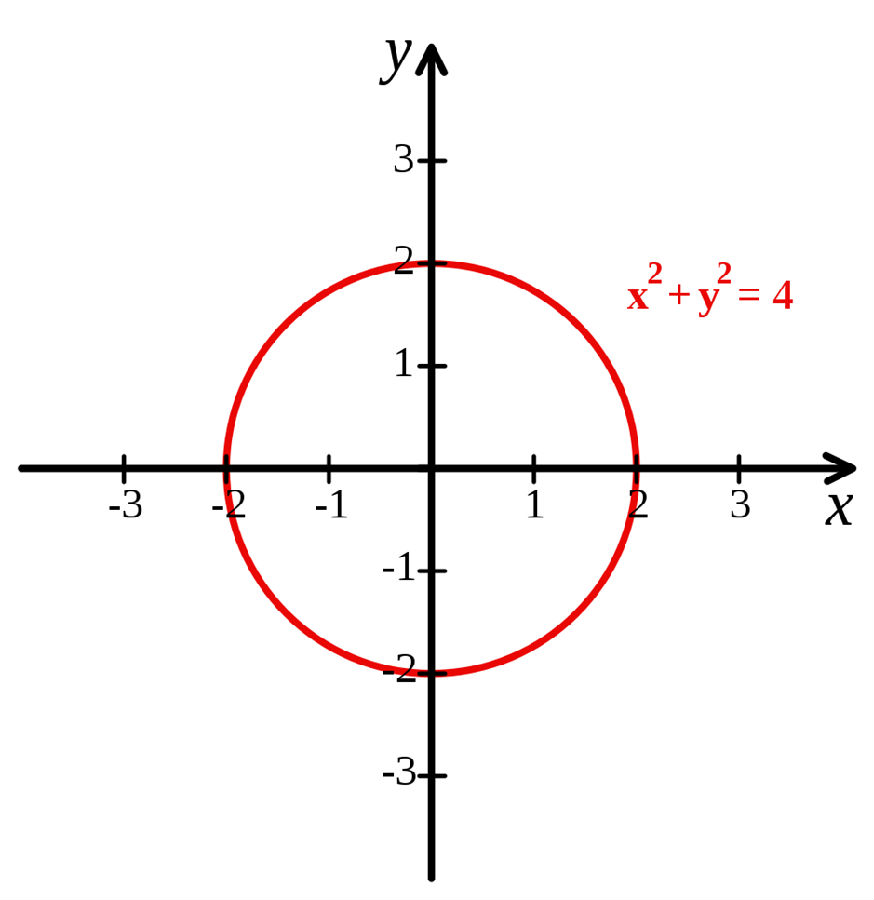
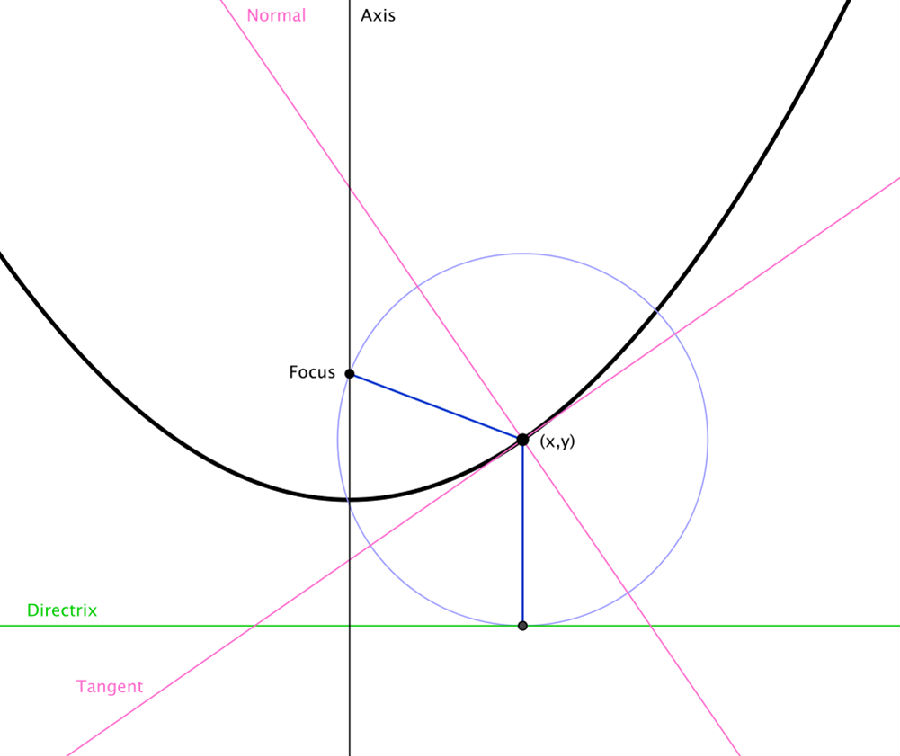
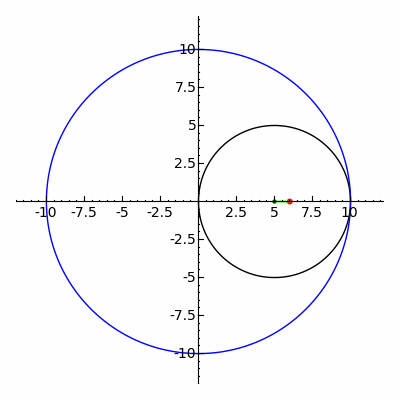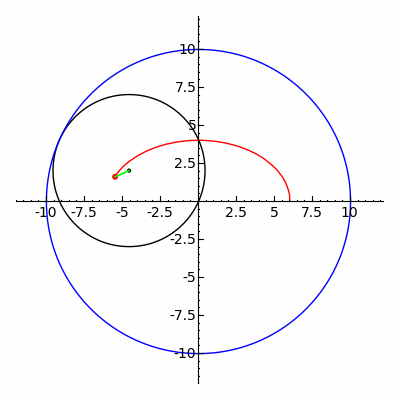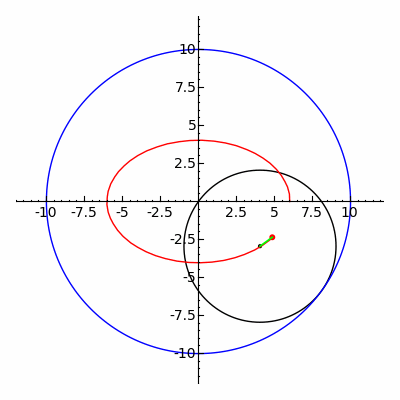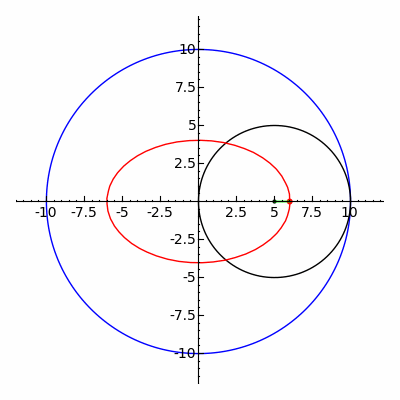
椭圆椭圆：土星环是圆形的，但部分看出，当......

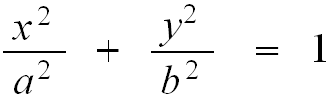
一个直角坐标系的一对数值坐标（x，y）的，这是有符号的距离从该点到两个固定的垂直导向线，长度为同一单元测量的指定的每个点独特地在一个平面上。各基准线被称为acoordinate轴或只是轴系统，并在它们满足点是它的起源，通常在有序对（0,0）的坐标系也可以被定义为点的垂直突起的位置上的两个轴，表示为从原点签名距离。

在一篇发表于1637年作为附录Discours德拉METHODE（话语的方法）的LaGéométrie，笛卡尔介绍了团结代数和几何成一个单一的主题，其中包括减少几何算术和代数形式的思想的新思路和新翻译几何形状成代数方程。但没有公式对后来被称为直角坐标系的坐标轴绘制在LaGéométrie。直角坐标的发明彻底改变了数学的解析几何的基础，以及许多其他的数学分支，如线性代数，复分析，微分几何，多元微积分，群论，更提供启发性的几何解释。