笛卡尔对数学最重要的贡献是创立了笛卡尔几何学。笛卡儿成功地将当时完全分开的代数和几何学联系到了一起。笛卡儿证明，几何问题可以归结成代数问题，可以通过代数转换来发现、证明几何性质。那么笛卡尔几何为什么又叫作“解析”几何哪？笛卡尔几何与前面反复强调的欧几里德几何有什么关系那？

“解析几何”英文为 Analytic Geometry，其中“解析”一词指的是数学分析Mathematic alanalysis术语中的“分析”，以微积分为基础。由于汉语西方学术名词翻译的混乱状态，弄的“解析几何”一语不知所云。

Mathematical analysis解析学

Analytic Geometry解析几何学

英文analysis提示我们笛卡尔几何在西方学术传统中属于分析类学科，那么欧几里德几何大概就属于analysis的反义词synthesis， 即“综合”类学科了。

康德将判断分成分析判断与综合判断：Analytic judgment is a judgment whose truth can be determined just by analyzing the term in it；Synthetic judgment is a judgment whose truth requires looking outside of its terms.

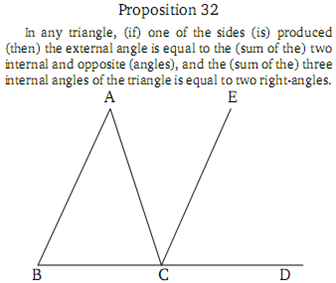
康德以欧几里德原本第一卷命题32的证明过程为例，对证明过程中用到的延长线和辅助平行线发难：这些突然冒出来的线是在哪里画出来的？答案只能是“空间”，那么康德问道：空间是什么东西？Space is the form of all possible perceptions。Space is a pure a priori intuition of the intellect.康德说：The judgment of Euclidean geometry are a priori synthetic。先验综合判断。而笛卡尔几何的分析判断性质完全来自数学分析的性质。康德有关欧几里德几何的分析十分接近柏拉图的深奥哲思，证实了本课程反复强调的观点：欧几里德原本是训练人的推理能力的必读教科书，不是一本数学工具书。而笛卡尔几何则由于采用数学分析而成为了实用技术，现代学子即便熟练地掌握了微积分运算，也一样可能是一个对逻辑推理一无所知的人。