即便公元1586年斯台文（西蒙Stevin）做了一项实验，否定了亚里士斯德的重物体比轻物体坠落得快的见解，这一实验曾经被人错误地说成是伽利略做的。斯台文写道：“反对亚里士多德的实验是这样的：让我们拿两只铅球，其中一只比另一只重十倍，把它们从三十尺的高度同时丢下来，落在一块木板或者什么可以发出清晰响声的东西上面，那么，我们会看出轻铅球并不需要比重铅球十倍的时间，而是同时落到木板上，因此它发出的声音听上去就象是一个声音一样。”在斯台文试验的几个世纪以后，阿波罗15号的宇航员在月球上使用一把锤子和一根羽毛重复了这个试验。这样的“实验”实际上是目测，或者说是与天文观测同样性质的“科学实验”，而不是爱因斯坦所说的科学的两大支柱之一的“文艺复兴时期发现进行系统的实验有可能找到自然现象之间的因果关系”。即便十四世纪的牛津计算者们导出默顿均速定律，奥利斯梅给出了默顿均速定律几何图形表示，伽里略在自由落体定律方面的几何数学理论结合实验验证研究依然是开启近代力学乃至开启科学实验的关键一步。

笛卡儿在1628年写道：“当我想到，为什么古代的那些早期的哲学先驱拒绝让那些不懂得数学的人研究学问，……我就怀疑到他们所拥有的那种数学知识和我们现在流行的数学是很不相同的，我越想越觉得如此。”到了十七世纪，数学已经成为科学方法的逻辑的一部分了；数学是研究事物性质的一种中立的工具，而不是事物性质的一种先天的决定因素。笛卡儿就是看出了数学在地位上发生的这种深刻变化的人。这种变化主要并不是出现在天文学上，而是在力学上。在力学上长期以来存在着一种技术实践和学术讨论的传统，而科学实验——数学方法就在力学上出现的。力学的科学和数学的实验方法与十六世纪先在意大利北部发展起来，这在当时的欧洲恐怕是工艺上最先进的地区，因为它拥有很多的名建筑师和工程师。艺术家兼工程师达·芬奇通过实验研究了种种建筑上的问题，他很懂得定量的实验在科学方法上的重要性，而且认识到了数学的价值。他写道：“科学上没有什么肯定的事情用不上一门数学科学的。”他觉得力学是最高贵的科学，“原因是通过力学，能动的生物才能作出所有的动作”。

古代力学的推翻和近代力学的建立是由帕多瓦大学和比萨大学的伽利略那样的人担当起来的。伽利略出生在比萨，在比萨读书并且在比萨的大学里教了一个短时期的书。他于公元1592年转到比较自由开明的帕多瓦大学任教，在那边待了十八年之久。他在力学方面的一些比较重要的研究都是在这个时期进行的。在公元1610年，他移居到佛罗伦撒，任托斯干大公爵的哲学和数学首席供奉并在佛罗伦萨用望远镜进行天文观测和研究。当他的天文学著作受到教廷谴责之后，他又重新研究起力学来了。伽利略指出，尽管工匠懂得很多，他们的知识并不是科学的，因为他们不熟悉数学，所以，他们不能从理论上发展成果。数学可以使其适应实物，并用来解释自然，这两者之间符合与否是由“选择得当的实验”来判断的。任何不符合的地方都是科学家的过错──“因此错误既不在抽象性，也不在几何学，也不在物理学，而在计算者；是计算者不懂得怎样算帐”。伽利略认为选择得当的数学证明可以用来探索任何牵涉到可量属性的问题，也就是几何学传统题材如长短、面积、体积等空间尺度之外的那些属性。在考察尺度效果时，伽利略就是以这个方式来研究物质的数量，即后来叫做质量的量，后来又以同样方式探索了牵涉到时间测量和速度测量的动力学问题。这是伽利略作为第一位亲自从事科学实验并且提供为后人所接受的科学理论的“科学家”，对于数学在科学中的作用的认识，也是科学中数学所起的关键作用的第一步，实际上从阿基米德就已经开始了。

伽利略的两部巨著是公元1632年出版的《关于托勒密和哥白尼两大世界体系的对话》和公元1638年出版的《论两种新科学》。两书都是采用对话形式，参与对话的是支持他的两个朋友，沙格列陀和萨尔维阿蒂，与一个亚里斯多德观点支持者辛普利邱（Simplicio - simple）。代表伽里略对现代科学的形成所建立的不朽功勋的是伽里略不顾宗教禁令在莱顿出版的最后的著作，当然也是科学史上最重要的经典之一：《论两种新科学》。

伽利略：Discorsiëdimostrazioni matematiche，intorno到期NUOVE scienze.1638年，晚于笛卡尔的话语和有关两门新科学的数学示威是伽利略的最后一本书安达排序的科学证明过的，涵盖了他从事物理研究工作前30标题命名years.The科学是材料的强度和objects.After他的对话关于两大世界体系，罗马宗教裁判所已经禁止发表任何工作，伽利略，包括任何他可能在写的议案future.After尝试发布工作在法国，德国和波兰的失败，它被拾起Lowys爱思唯尔在莱顿，荷兰，那里的宗教裁判所的令状是很少考虑的。荷兰出大家的秘密在这！

伽利略想要用这种对话形式使他的著作能拥有广大的读者，从而能有效地否定掉亚里斯多德的力学和宇宙论。伽利略在力学上的工作，和斯台文等人的工作一样，是被工程上的问题激起的。他在1632年写的一封信中提到抛射体的射程问题使他开始从事研究物体重力坠落。

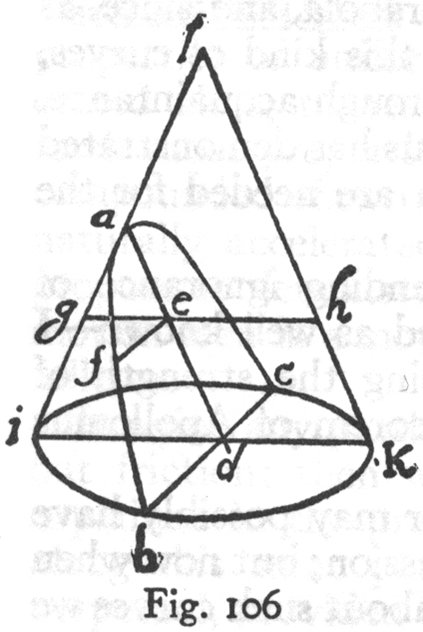
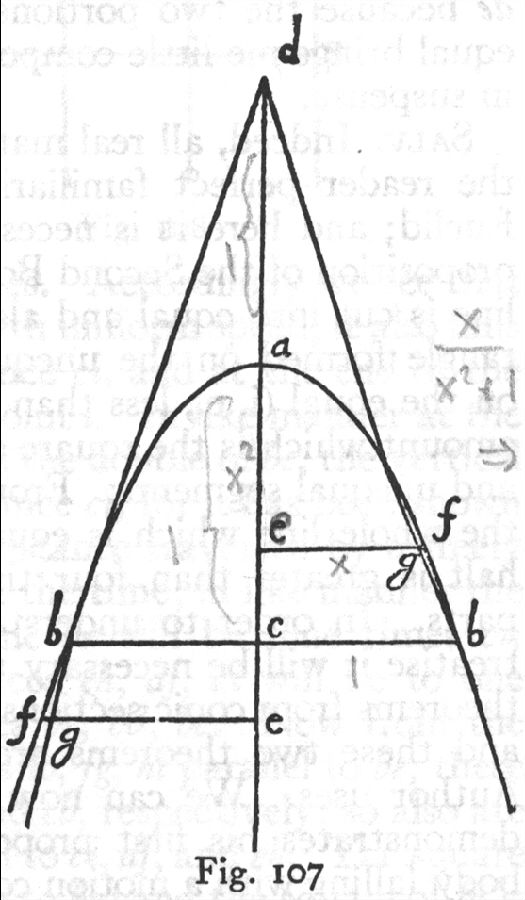
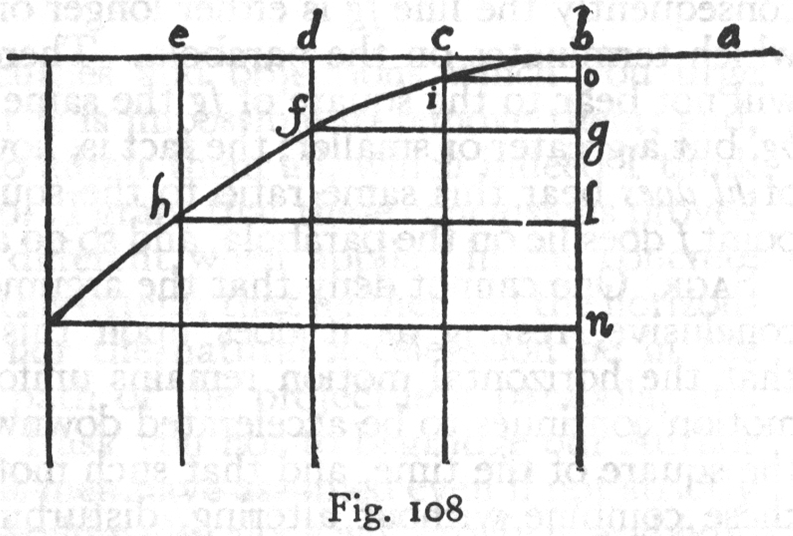
伽利略的《论两种新科学》第四天的对话集中讨论了抛射体(projectile)的运动的抛物线(parabola)轨迹的数学（欧几里德几何学）证明。

定理1，定理I：这是由一个均匀的水平运动混有一个自然加速垂直运动进行甲弹丸说明这是一个半抛物线的路径。 

定理2，定理II：当一个物体的运动是两个均匀的运动，一个水平，其它垂直的生成物中，为所得到的动量的平方等于两个分量动量的平方的总和。

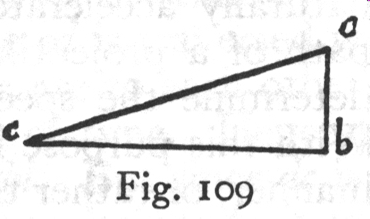
爱因斯坦：“这么大的一个物理学的贡献是两门新科学的学者长期以来坚持认为，这本书预计的议案艾萨克牛顿定律。”