第一定律：

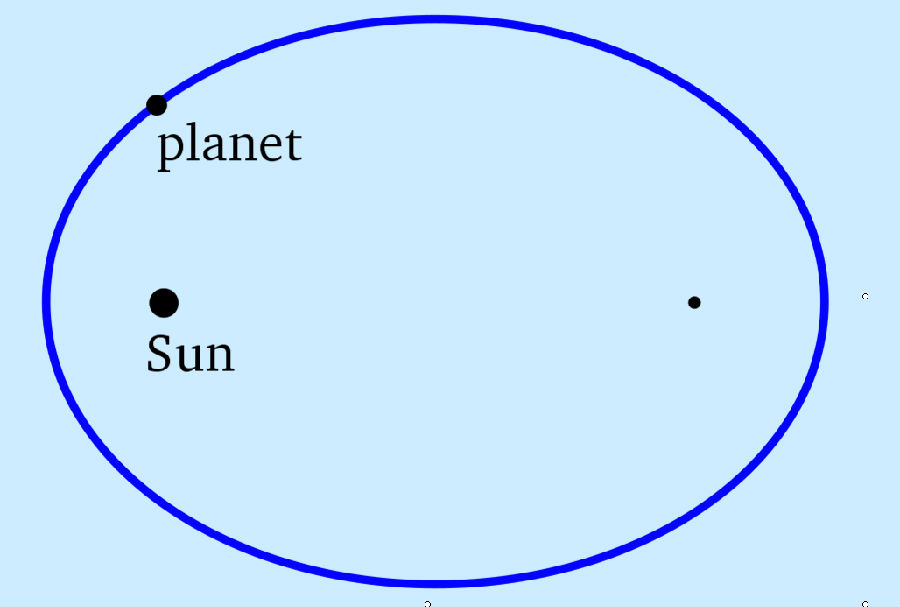
“每颗行星的轨道是一个椭圆与太阳在两个中的一个foci."每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中。

第二定律：

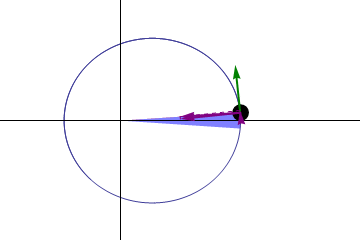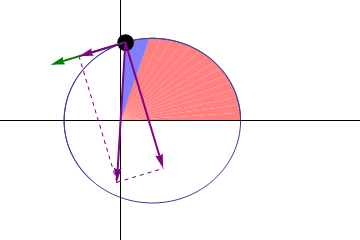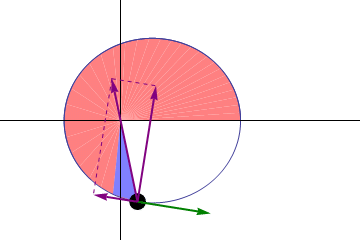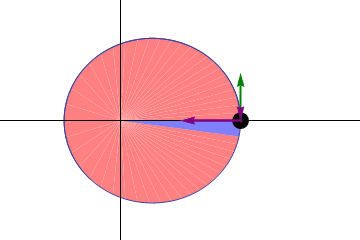
“一条线连接的行星和太阳的期间相等的间隔内扫过相等的面积time."在相等时间内，太阳和运动中的行星的连线（向量半径）所扫过的面积都是相等的。这一定律实际揭示了行星绕太阳公转的角动量守恒。

第三定律：

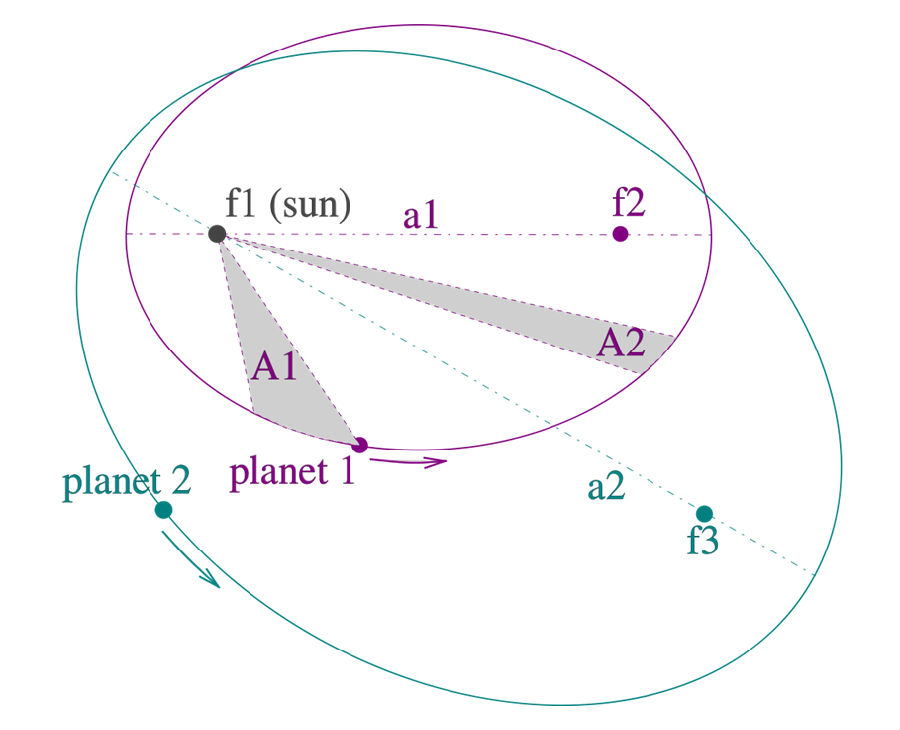
“行星的公转周期的平方成正比的半长轴的立方的orbit."开普勒第三定律，也称调和定律，也称周期定律：是指绕以太阳为焦点的椭圆轨道运行的所有行星，其椭圆轨道半长轴的立方与周期的平方之比是一个常量。

第谷的数据中对火星的观测占有最大篇幅，而这个行星的运行与哥白尼理论出入最大。开普勒按照传统的偏心圆来探求火星的轨道。开普勒计算出来的火星位置和第谷数据之间相差的角度相当于表上的秒针在0.02秒瞬间转过的角度。开普勒完全信赖第谷观测的辛勤与精密，即使是这样微小的数值，第谷也是不可能弄错的。开普勒意识到始终无法找出一个符合第谷观测数据的圆形轨道后，他就大胆摒弃这种古老的匀速圆周运动的偏见，尝试用别的几何曲线来表示所观测到的火星的数据。开普勒认为行星运动的焦点应在施引力的中心天体——太阳的中心，火星运动的线速度是变化的，而这种变化应当与太阳的距离有关：靠近太阳时，速度最快；远离太阳时，速度最慢。还是几何学帮了天文学的大忙。假使没有古希腊人对圆锥曲线的研究，开普勒的定律不可能被发现。椭圆是圆锥曲线的一种，它的形状使开普勒想到火星可能在这样一种曲线的轨道上运动。

1609年，开普勒发表《新天文学》一书和《论火星运动》一文，公布了前两个定律。