力学（希腊Μηχανική）的两个主要子字段是经典力学和量子力学。

经典力学关注的是一套描述forces.During近代早期的系统的作用下物体运动的物理定律，科学家如伽利略，开普勒和牛顿尤其是，奠定了现在被称为经典mechanics.不幸牛顿与莱布尼茨各自发明微分学以后，符号既不相同，又在发明先后问题上发生争执，因此事情就复杂化了。由于这些原因中的一个或两个原因，英国数学家与大陆数学家就分道扬镳了。前者用了牛顿的符号，但大半疏忽了他的新分析方法，而遵循牛顿常用以记载他的研究结果的几何学方法。因此，英国学派对于十八世纪前半期新微积分学的发展很少贡献，但在大陆上，特别是在詹姆斯·伯努利的手里，微积分学却得到发展。牛顿的工作成果由莫佩尔蒂等人的著作介绍到法国去，更由达朗贝尔、克勒洛（Clairault）与欧拉加以发展。特别是经过法国的三L的工作，力学才最终形成了目前的古典力学体系，名为分析力学。

莫佩屠斯莫佩尔蒂

1698年至1759年

夏特莱侯爵夫人的老师

贡献：地球的形状，最小作用量原理。

牛顿由秒摆长度的差异推论赤道处的引力比两极附近引力小，即地球是一个扁平的球，在两极较平，在赤道则凸出来。莫佩尔蒂率领一支远征队测量出经度一度的长度，彻底地证明了地球是近扁球形的。

至少动作原理指出，在所有的自然现象被称为“动作”的数量趋于最小化。莫佩屠斯开发了这样的原则，超过二十年。

1741年，莫佩尔蒂在巴黎科学院发表论文表明，在一个系统里，所有呈静止状态的物体，假若有任何变化，产生的运动，趋向于作用量的最小改变。为了形而上学的理由，假定在光的传播这样的过程中，必定有某种东西是个最小量。他指出事实竟与光循最小作用的路径传播的假定一致。  

约瑟夫·路易斯·拉格朗日拉格朗日

1736年至1813年

法国数学家，天文学家，分析力学，天体力学。

拉格朗日把这个原理推广到一切物体的运动上去，而把“作用量”定义为运动量的空间积分，或动能的时间积分的两倍，建立了古典力学的“分析力学”体系，物理学界称为拉格朗日力学。

拉格朗日总结了18世纪的数学成果，同时又为19世纪的数学研究开辟了道路，堪称法国最杰出的数学大师。同时，他的关于月球运动（三体问题）、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果，在使天文学力学化、力学分析化上，也起到了历史性的作用，促进了力学和天体力学的进一步发展，成为这些领域的开创性或奠基性研究。

莱昂哈德保罗·欧拉欧拉

1707-1783

瑞士数学家，物理学家

拉格朗日导师

世界上最美的公式：欧拉公式

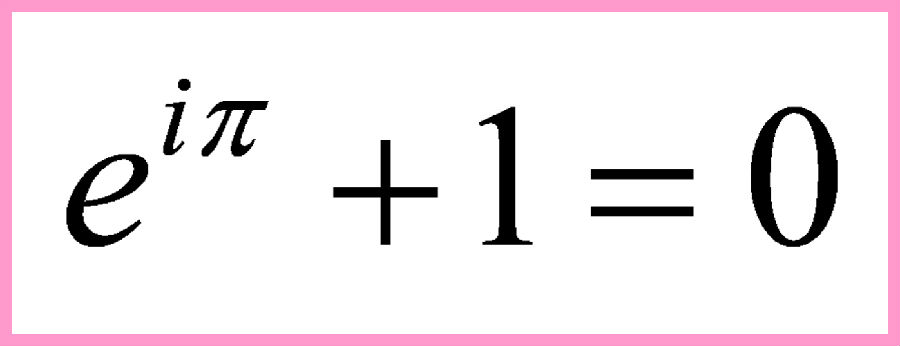
欧拉是18世纪数学界最杰出的人物之一，他不但为数学界作出贡献，更把数学推至几乎整个物理的领域。他是数学史上最多产的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学、变分法等的课本，《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学中的经典著作。欧拉对数学的研究如此广泛，因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。此外欧拉还涉及建筑学、弹道学、航海学等领域。瑞士教育与研究国务秘书Charles Kleiber曾表示：“没有欧拉的众多科学发现，今天的我们将过着完全不一样的生活。”法国数学家拉普拉斯则认为：读读欧拉，他是所有人的老师。

达朗贝尔达朗贝尔

717-1783

法国数学家，力学家，天文学家

“百科全书”编辑

达朗贝尔一生研究了大量课题，完成了涉及多个科学领域的论文和专著，其中最著名的有八卷巨著《数学手册》、力学专著《动力学》、23卷的《文集》、《百科全书》的序言等等。

数学是达朗贝尔研究的主要课题，他是数学分析的主要开拓者和奠基人。达朗贝尔为极限作了较好的定义，但他没有把这种表达公式化。波义尔做出这样的评价：达朗贝尔没有摆脱传统的几何方法的影响，不可能把极限用严格形式阐述；但他是当时几乎唯一一位把微分看成是函数极限的数学家。

达朗贝尔是十八世纪少数几个把收敛级数和发散级数分开的数学家之一，并且他还提出了一种判别级数绝对收敛的方法——达朗贝尔判别法，即现在还使用的比值判别法；他同时是三角级数理论的奠基人；达朗贝尔为偏微分方程的出现也做出了巨大的贡献，1746年他发表了论文《张紧的弦振动是形成的曲线研究》，在这篇论文里，他首先提出了波动方程，并于1750年证明了它们的函数关系；1763年，他进一步讨论了不均匀弦的振动，提出了广义的波动方程；另外，达朗贝尔在复数的性质、概率论等方面也都有所研究，而且他还很早就证明了代数基本定理。

达朗贝尔在数学领域的各个方面都有所建树，但他并没有严密和系统的进行深入的研究，他甚至曾相信数学知识快穷尽了。但无论如何，十九世纪数学的迅速发展是建立在他们那一代科学家的研究基础之上的，达朗贝尔为推动数学的发展做出了重要的贡献。

达朗贝尔认为力学应该是数学家的主要兴趣，所以他一生对力学也作了大量研究。达朗贝尔是十八世纪为牛顿力学体系的建立作出卓越贡献的科学家之一。

《动力学》是达朗贝尔最伟大的物理学著作。在这部书里，他提出了三大运动定律，第一运动定律是给出几何证明的惯性定律；第二定律是力的分析的平行四边形法则的数学证明；第三定律是用动量守恒来表示的平衡定律。书中还提出了达朗贝尔原理，它与牛顿第二定律相似，但它的发展在于可以把动力学问题转化为静力学问题处理，还可以用平面静力的方法分析刚体的平面运动，这一原理使一些力学问题的分析简单化，而且为分析力学的创立打下了基础。

皮埃尔·西蒙·拉普拉斯拉普拉斯

1749年至1727年

法国数学家，天体力学集大成者

拉普拉斯是法国分析学家、概率论学家和物理学家，法国科学院院士。1749年3月23日生于法国西北部卡尔瓦多斯的博蒙昂诺日，1827年3月5日卒于巴黎。1816年被选为法兰西学院院士，1817年任该院院长。1812年发表了重要的《概率分析理论》一书，在该书中总结了当时整个概率论的研究，论述了概率在选举审判调查、气象等方面的应用，导入“拉普拉斯变换”等。他致力于挽救世袭制的没落：他当了六个星期的拿破仑的内政部长，后来成为元老院的掌玺大臣，并在拿破仑皇帝时期和路易十八时期两度获颁爵位，后被选为法兰西学院院长。拉普拉斯曾任拿破仑的老师，所以和拿破仑结下不解之缘。

拉普拉斯把注意力主要集中在天体力学的研究上面。他把牛顿的万有引力定律应用到整个太阳系，1773年解决了一个当时著名的难题：解释木星轨道为什么在不断地收缩，而同时土星的轨道又在不断地膨胀。拉普拉斯用数学方法证明行星平均运动的不变性，即行星的轨道大小只有周期性变化，并证明为偏心率和倾角的3次幂。这就是著名的拉普拉斯定理。此后他开始了太阳系稳定性问题的研究。同年，他成为法国科学院副院士。

1784—1785年，他求得天体对其外任一质点的引力分量可以用一个势函数来表示，这个势函数满足一个偏微分方程，即著名的拉普拉斯方程。1785年他被选为科学院院士。1786年证明行星轨道的偏心率和倾角总保持很小和恒定，能自动调整，即摄动效应是守恒和周期性的，不会积累也不会消解。拉普拉斯注意到木星的三个主要卫星的平均运动Z ₁，Z ₂，Z ₃服从下列关系式：Z ₁ -3×Z ₂ +2×Z ₃ =0。同样，土星的四个卫星的平均运动Y ₁，Y ₂，Y ₃，Y ₄也具有类似的关系：5×Y ₁ -10×Y ₂ +Y ₃ +4×Y ₄ =0。后人称这些卫星之间存在可公度性，由此演变出时间之窗的概念。

1787年发现月球的加速度同地球轨道的偏心率有关，从理论上解决了太阳系动态中观测到的最后一个反常问题。1796年他的著作《宇宙体系论》问世，书中提出了对后来有重大影响的关于行星起源的星云假说。在这部书中，他独立于康德，提出了第一个科学的太阳系起源理论——星云说。康德的星云说是从哲学角度提出的，而拉普拉斯则从数学、力学角度充实了星云说，因此，人们常常把他们两人的星云说称为“康德—拉普拉斯星云说”。

他长期从事大行星运动理论和月球运动理论方面的研究，尤其是他特别注意研究太阳系天体摄动，太阳系的普遍稳定性问题以及太阳系稳定性的动力学问题。在总结前人研究的基础上取得大量重要成果，他的这些成果集中在1799—1825年出版的5卷16册巨著《天体力学》之内。在这部著作中第一次提出天体力学这一名词，是经典天体力学的代表作。因此他被誉为法国的牛顿和天体力学之父。1814年拉普拉斯提出科学假设，假定如果有一个智能生物能确定从最大天体到最轻原子的运动的现时状态，就能按照力学规律推算出整个宇宙的过去状态和未来状态。后人把他所假定的智能生物称为拉普拉斯妖。

他发表的天文学、数学和物理学的论文有270多篇，专著合计有4006多页。其中最有代表性的专著有《天体力学》、《宇宙体系论》和《概率分析理论》（1812年发表）。

阿德里安·玛丽·勒让德勒让德

1752年至1833年

法国数学家

勒让德的主要研究领域是分析学（尤其是椭圆积分理论）、数论、初等几何与天体力学，取得了许多成果，导致了一系列重要理论的诞生。勒让德是椭圆积分理论奠基人之一。在欧拉提出椭圆积分加法定理后的40年中，他是仅有的在这一领域提供重大新结果的数学家。但他未能像NH阿贝尔和CGJ雅可比那样洞察到关键在于考察椭圆积分的反函数，即椭圆函数。在关于天文学的研究中，勒让德引进了著名的“勒让德多项式” ，发现了它的许多性质。他还研究了B函数和Γ函数，得到了Γ函数的倍量公式。他陈述了最小二乘法，提出了关于二次变分的“勒让德条件”。

勒让德对数论的主要贡献是二次互反律，这是同余式论中的一条基本定理。他还是解析数论的先驱者之一，归纳出了素数分布律，促使许多数学家研究这个问题。

“3L”：法国18世纪后期到19世纪初数学界著名的三个人物：勒让德（阿德里安·玛丽·勒让德），拉格朗日（约瑟夫路易斯拉格朗日）和拉普拉斯（皮埃尔·西蒙laplace)三个人的姓氏的第一个字母为“L”，又生活在同一时代，所以人们称他们为“三L”。

在埃菲尔铁塔上共刻有72个法国科学家、工程师与其他知名人士的名字，居斯塔夫·埃菲尔以此来铭记他们做出的贡献。这些雕刻都位于铁塔第一个平台下方四周的壁面上，每个字母约60厘米高，且只刻有每个人的姓。雕刻最初于20世纪初期完成，不过在1986年至1987年间，负责艾菲尔铁塔运营的新艾菲尔铁塔开发公司（Société中篇小说D'开采德拉埃菲尔铁塔）重修了这些雕刻。

       威廉爵士罗文汉密尔顿哈密顿      

1805-1865

爱尔兰物理学家     

天文学家   

数学家

哈密顿的父亲阿其巴德（罗文阿奇博尔德Hamilton)为都柏林市的一个初级律师。哈密顿自幼聪明，被称为神童。他三岁能读英语，会算术；五岁能译拉丁语、希腊语和希伯来语，并能背诵荷马史诗；九岁便熟悉了波斯语，阿拉伯语和印地语。14岁时，因在都柏林欢迎波斯大使宴会上用波斯语与大使交谈而出尽风头。

哈密顿工作勤奋，思想活跃。他发表的论文一般都很简洁，别人不易读懂，但手稿却很详细，因而很多成果都由后人整理而得。仅在三一学院图书馆中的哈密顿手稿，就有250本笔记及大量学术通信和未发表论文。爱尔兰国家图书馆还有一部分手稿。

他的研究工作涉及不少领域，成果最大的是光学、力学和四元数。他研究的光学是几何光学，具有数学性质；力学则是列出动力学方程及求解；因此哈密顿主要是数学家。但在科学史中影响最大的却是他对力学的贡献，哈密顿量是现代物理最重要的量，当我们得到哈密顿量，就意味着得到了全部。

动作功能：

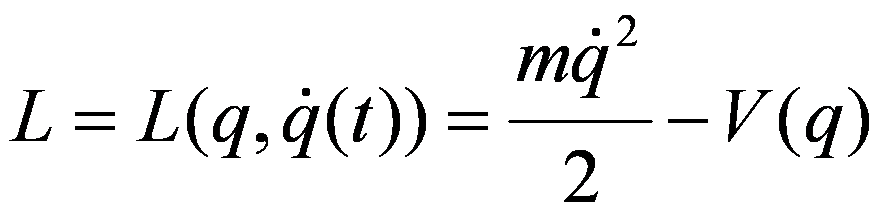
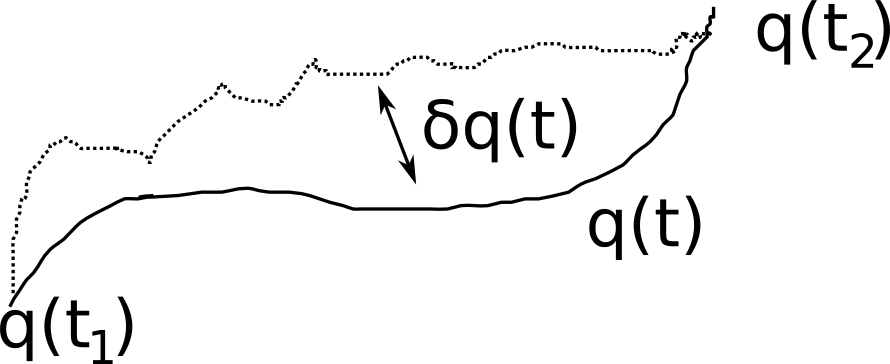
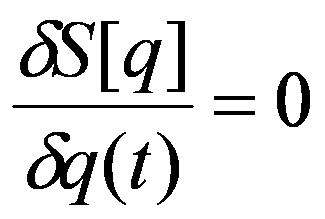
欧拉 - 拉格朗日方程：

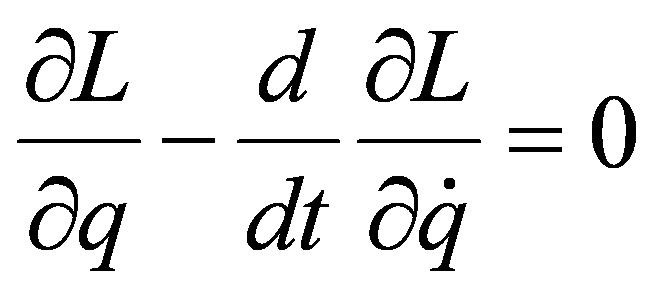
勒让德变换：

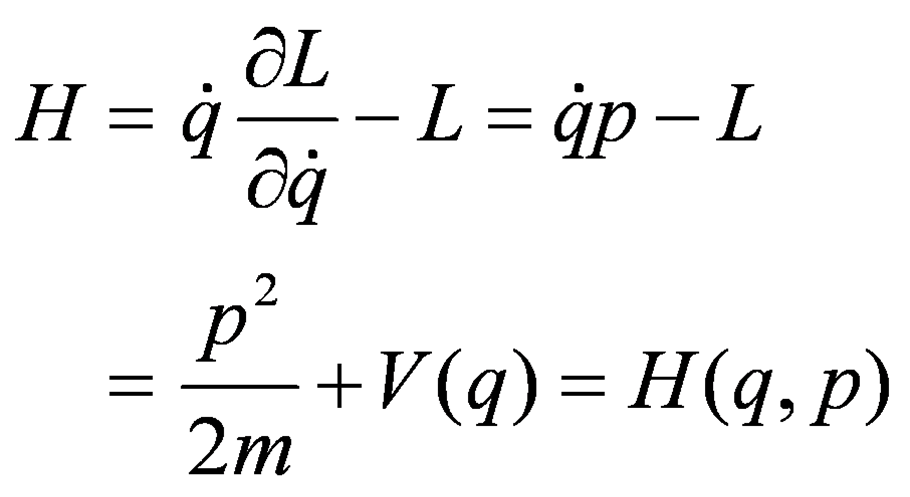
Hamilton方程：

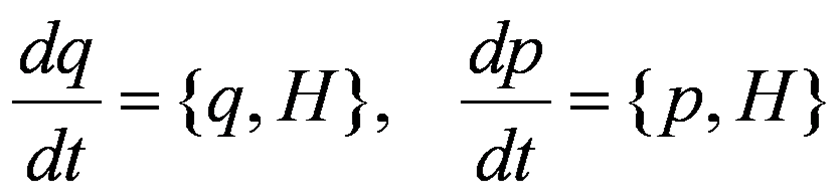
泊松括号：

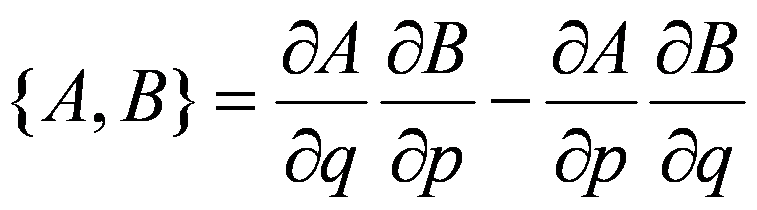
在直角坐标系标准依据：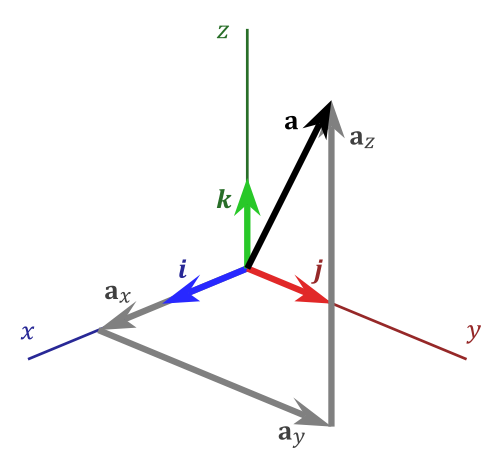

相当于在标准的基础载体。

这是由爵士Hamiltonin 1843推出。

相关链接：古典力学体系的形成