The basic domains of physics:

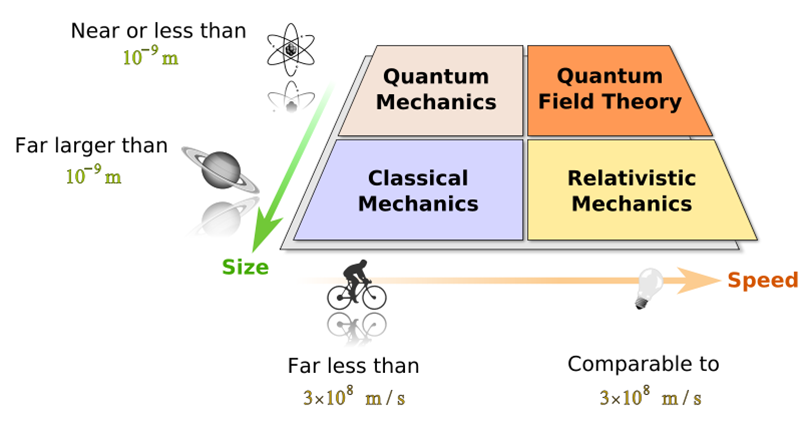
The sum total of our physical knowledge of the universe is contained in two theories:relativity and quantum theory.This is the crowning achievement of 2600 years of investigation into the universe,since the time of the Greeks.Physics is also called"the fundamental science" because the subject of study of all branches of natural science like Chemistry,Astronomy,Geology and Biology are constrained by laws of physics.

Mathematics is the language used for compact description of the order in nature, especially the laws of Physics.This was noted and advocated by Pythagoras,Plato,Archimedes,Alhazen,Galileo,Newton,Maxwell,Einsteinand Dirac.

Ontology is a prerequisite for Physics,but not for Mathematics.It means Physics is ultimately concerned with descriptions of the real world,while Mathematics is concerned with abstract patterns,even beyond the real world.Thus Physics statements are synthetic,while Math statements are analytic.Mathematics contains hypothesis,while Physics contains theories.Mathematics statements have to be only logically true, while predictions of Physics statements must match observed and experimental data.

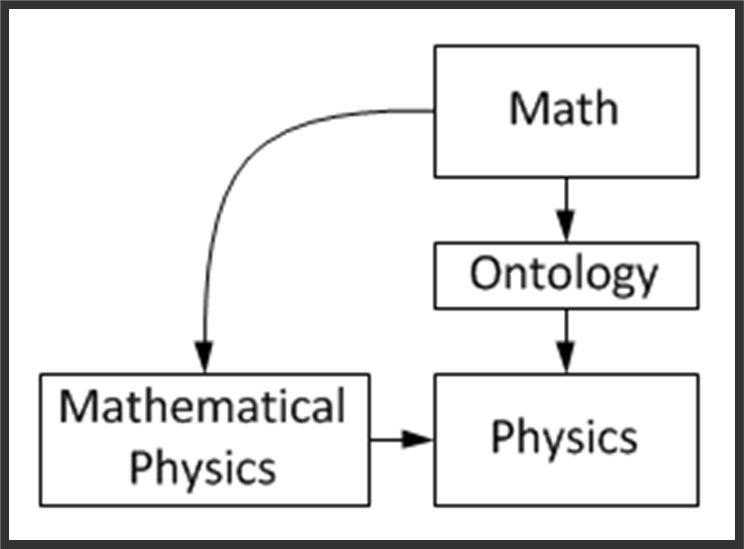
The distinction is clear-cut,but not always obvious. For example, Mathematical Physics is the application of Mathematics in Physics.

David Hilbert

（1862—1943）

recognized as one of the most influential and universal mathematicians

He discovered and developed a broad range of fundamental ideas in many areas,including invariant theory and the axiomatization of geometry.

General theory of relativity

He also formulated the theory of Hilbert spaces,one of the foundations of functional analysis.

1943年（希尔伯特去世的那一年），他在一次宴会上与纳粹教育部长相邻而坐。部长问他：“摆脱了犹太人的影响，哥廷根的数学现在怎么样？”希尔伯特：“哥廷根的数学？实际上哥廷根已经没有一点儿数学了！”

希尔伯特墓志铭：Wir müssen wissen.Wir werden wissen.In English:We must know.We will know.

Hilbert:"Physics is too hard for physicists."（Hilbert 语录：“上课不许讲教材里的东西。”）

Einstein said:Physical concepts are free creations of the human mind.

Our experience hither to justifies us in trusting that nature is the realization of the simplest that is mathematically conceivable……But the actual creative principle lies in mathematics.Thus,in a certain sense, I take it to be true that pure thought can grasp the real,as the ancients had dreamed.