任务4：点的投影

2学时

任务主要内容：通过学习，能正确描述点的三面投影的形成；能依据点的坐标绘制点的三面投影图；能正确判断两点间的相互位置。

点的三面投影：

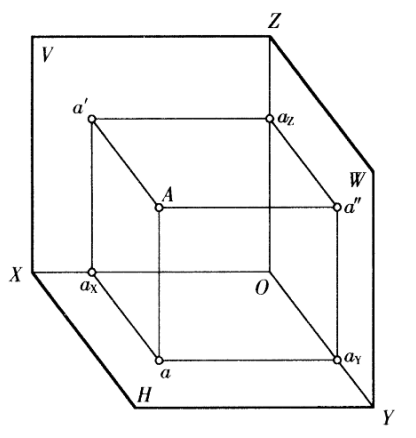
一、点的三面投影图的形成

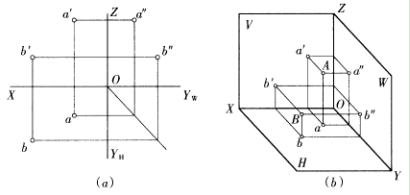
如下图所示，将空间点A置于三面投影体系中，采用正投影的方法，自A点分别向三个投影面作投影线(作垂线)，分别与投影面相交得a、a′、a″，即为空间点A的H面投影、Y面投影和W面投影。则：

A点在H面上的投影a→称为空间点A的水平投影；

A点在Y面上的投影a′→称为空间点A的正面投影；

A点在W面上的投影a″→称为空间点A的侧面投影。

二、点的投影规律

点的投影也依然符合三面投影的规律：长对正、高平齐、宽相等，如下图所示。

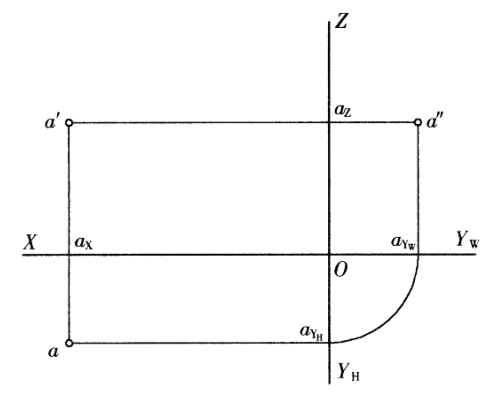
三、根据点的两面投影，完成其的第三面投影

点的坐标：

一、点的投影与坐标

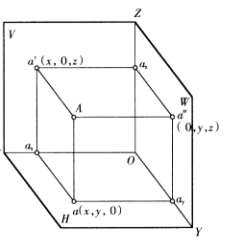
在三面投影体系中，点A的位置可以由它到三个投影面的距离来表示，也可用直角坐标来表示。如下图所示。

空间点的坐标——A（x，y，z）：

    A点到W面的距离 = a″A = Oa_X = X坐标

    A点到V面的距离 = a′A = Oa_Y = Y坐标

    A点到H面的距离 = aA = Oa_Z = Z坐标

二、已知A（6,4,7），求A点的三面投影图

三、根据A点的三面投影图，求A点的坐标

两点间的相互位置：

一、两点的相对位置

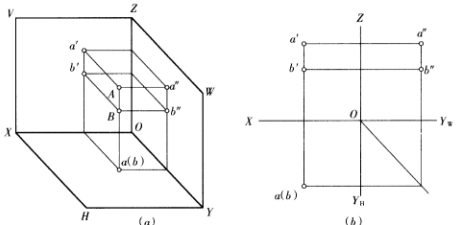
空间两点相对位置，可根据两点的三个坐标进行判别，如下图所示。由方位规律可知，X轴坐标表示左右方向，X_a＜X_b。Y轴坐标表示前后方向，Y_a＜Y_b。Z轴表示上下方向，Z_a＞Z_b。所以A点在B点的右、后、上方。

二、重影点及其可见性的判断

空间两点位于某一投影方向的同一投影线上时，则两点的投影重合，这两个点被称为对该投影面的一对重影点。如下图所示，A、B两点在同一投影线上，且A点在B点之上，则H面a、b两投影重合，此重合投影称为H面的重影，其他两投影不重合。a、b两投影的可见性可从V面投影和W面投影进行判别。在V面上a′高于b′(在W面上a″高于b″)，故A点在上，B点在下，A点可见，B点不可见。为了区别起见，不可见的重影点的代号写在可见点的后面，并加圆括号表示。