任务5:直线的投影
6学时
任务主要内容:通过学习,能正确识别直线与投影面之间的关系、能正确绘制直线的三面投影;能正确绘制直线的实长;能正确判断点是否在直线上;能正确识别两直线的相互关系。
直线投影的形成:
一、直线的投影
直线是点沿着一定方向运动的轨迹。两点即可定一直线。求作直线的投影就是求作直线两个端点的投影,然后同名投影连线,即得该直线的投影。
例题1.已知A、B两点坐标,求AB直线的三面投影
例题2.已知直线的两面投影,求第三面投影
二、直线对投影面的倾角
直线与投影面上的投影所夹的角,称为直线对该投影面的倾角。按照规定,对H、V、W面的倾角分别用α、β、γ表示。
三、直线与投影面的相对位置
按照直线与投影面相对位置的不同分为:一般位置直线、特殊位置直线。特殊位置直线又分为:投影面的平行线和投影面的垂直线。
课后测试:
投影面垂直线:
一、概念
垂直一个投影面与另外两个投影面平行的直线,称为投影面的垂直线。它有三种情况:
(1)与H面垂直的直线,称为铅垂线;
(2)与V面垂直的直线,称为正垂线;
(3)与W面垂直的直线,称为侧垂线。
二、投影特性
投影面垂直线的投影特性是:
(1)与哪一个投影面垂直,在该投影面上的投影积聚成一个点;
(2)另外两个投影面的投影分别反映直线的实长,且投影平行于同一个投影轴。
课后测试:
投影面平行线:
一、概念
平行一个投影面与另外两个投影面倾斜的直线,称为投影面的平行线。它有三种情况:
(1)与H面平行的直线,称为水平线;
(2)与V面平行的直线,称为正平线;
(3)与W面平行的直线,称为侧平线。
二、正平线的投影特性
三、水平线的投影特性
四、侧平线的投影特性
五、投影面平行线的共性
投影面平行线的投影特性是:
(1)与哪一个投影面平行,则在该投影面上的投影反映实长,反映直线对其他两个投影面的真实倾角;
(2)另外两个投影分别平行相对应的投影轴,且不反应实长。
课后测试:
一般位置直线:
一、概念
倾斜于三个投影面的直线,称为一般位置直线。
二、投影特性
一般位置直线的投影特性:
(1)直线的三个投影仍为直线,且均小于实长。
(2)直线的三个投影倾斜于投影轴,三个投影与投影轴的夹角不反映直线与投影面的真实倾角α、β、γ。
三、一般位置直线的实长
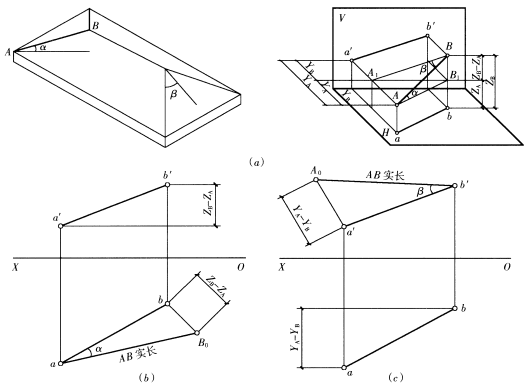
一般位置直线的三面投影即不反映实长,也不反映真实倾角,但可以通过直角三角形法,求得空间直线的实长和真实倾角,如下图所示。
如下图(a)所示,过A点做AB1∥ab,则Aa=B1b=ZA,BB1=ZB-ZA(A、B两点的Z轴坐标差),AB1∥ab,已知直角三角形的两直角边,则斜边为实长,∠BAB1为所求的倾角α,这种方法称为直角三角形法。
如下图(b)所示,过b点作ab的垂线,取长度等于ZB-ZA,连接三角形,则斜边aB0为所求实长,∠baB0为所求倾角α。同理,可在v面投影图上求实长和倾角β,如下图(c)所示。
例题1.已知一般位置直线的V面和H面投影,求直线的实长及直线对H面的倾角。
例题2.已知直线AB的实长为6,并已知直线的V面投影和A点的H面投影,求该直线的H面投影。
课后测试:
直线上的点:
点在直线上,点一定在直线的同面投影上。根据这一投影特性,我们就可以从三面投影中判别点是否在直线上。
例题1.判断M点是否在直线AB上
例题2.已知直线的V面投影和H面投影,及直线上K点的H面投影,求K点的V面投影。
两直线的相对位置:
一、概念
空间两直线的相对位置有三种情况:两直线平行、两直线相交、两直线交叉。
二、平行两直线
空间两直线平行,它们的同名投影一定平行。
例题1.补全下列两平行线的H面投影。
三、相交两直线
空间两直线相交,它们的同名投影一定相交,交点为两直线的公共点,且交点符合点的投影规律。
例题2.已知两条直线的两个投影,判断在空间这两条直线是否相交。
四、交叉两直线
在空间既不平行也不相交的两直线,称为交叉两直线,又称异面直线。
**拓展学习:两直线垂直交叉**
空间垂直相交两直线,其中一条直线平行于投影面时,则两直线在该投影面上的投影为直角(称为直角投影定理)。
例题:求A点到水平线EF的距离。


