任务6：平面的投影

6学时

任务主要内容：通过学习，能正确识别平面与投影面之间的位置关系、能正确绘制各种平面的三面投影；能正确绘制直线的实长；能正确判断点是否在直线上；能正确识别两直线的相互关系。

一般位置平面：

一、平面的表示法

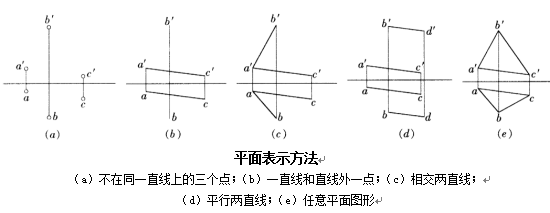
    不在一条直线上的三个点，即可确定一个平面。因此，表示平面的方法如下图所示。

二、平面与投影面的相对位置

    依据平面与投影面的位置关系不同，可分为：一般位置平面、投影面平行面、投影面垂直面。

三、一般位置平面

    与三个投影面都倾斜的平面，称为一般位置平面。

    一般位置平面的投影特性是：三个投影均成平面形，比实际形状小，不反映实形。

投影面平行面：

一、概念

    平行于一个投影面，与另外两个投影面垂直的平面，称为投影面的平行面。它有三种情况：

   （1）与V面平行的平面，称为正平面；

   （2）与H面平行的平面，称为水平面；

   （3）与W面平行的平面，称为侧平面。

二、投影特性

    投影面平行面的投影特性是：

   （1）与哪一个投影面平行，在该投影面上的投影反映实形；

   （2）另外两个投影积聚成直线段，且共同垂直于相对应的投影轴(平行于相对应的投影轴)。

投影面垂直面：

一、概念   

    垂直于一个投影面，与另外两个投影面倾斜的平面，称为投影面的垂直面。它有三种情况：

   （1）与V面垂直的平面，称为正垂面；

   （2）与H面垂直的平面，称为铅垂面；

   （3）与W面垂直的平面，称为侧垂面。

二、投影特性   

   投影面垂直面的投影特性是：

   （1）与哪一个投影面垂直，在该投影面上的投影积聚成一条直线，且反映对其他两个投影面的真实倾角；

   （2）另外两个投影均成平面形，但比实际形状小。

平面上的点：

一、点在平面上的几何判定条件

    如果点在平面内的任一直线上，则点一定在该平面上。

   

例题1：求三角形平面上K点的V面投影。

例题2：判断M点是否在三角形ABC平面上。

例题3：不全四边形平面的H面投影。

直线与平面平行：

    若直线平行于平面上的任一直线，则此直线必与该平面平行。

例题1：判断MN直线是否平行于四边形平面ABCD。

例题2：过M点做一条水平线平行于三角形平面ABC。

平面与平面平行：

    若一平面上的一对相交直线与另一平面上的一对相交直线对应平行，则该两平面平行。

例题1：过K点作一个平面与已知三角形平面平行。

直线与平面相交、平面与平面相交：

    直线与平面或平面与平面之间，若不平行则必相交。

积聚法求交点、交线：

例题1：求正垂面与一般位置直线的交点。

例题2：求一般位置平面与正垂线的交点。

例题3：求正垂面与一般位置平面的交线。

辅助平面法求交点、交线：

例题4：求一般位置直线与一般位置平面的交点。

例题5：求两个一般位置平面的交线。