 Unit Analysis
Unit Analysis
单位分析
Implications
启示
Physics can often become confusing becausephysical quantities are often expressed in terms of different units. Forexample the speed of light is
物理常常会变得混乱,因为物理量经常用不同的单位表示。例如,光的速度是
c=186000 Mps=299000000 m/s=1light-second/second
c = 186000 英里/秒 = 299000000米/秒= 1光秒/秒
Understanding the meaning of units isimportant for two reasons: it allows us to determine the dimensions of physicalquantities, and to understand the scale of physical phenomena.
理解单位的意义很重要,有两个原因:它使我们能够确定物理量的维度,并理解物理现象的尺度。
In physics, the number associated with a physical quantity is meaningless unless the units are specified.
在物理学中,与物理量相关的数字是没有意义的,除非指定了单位。
Units are not only useful in understanding the scale of a physical quantity, but also in determining its dimensions.
单位不仅有助于理解物理量的规模,而且可以确定其维度。
Scientific Notation
科学记数法
Because we will constantly encounter numbers, we want to be able to express them in the most concise way possible. It is quite cumbersome to write a small number as: 0.000000000001. How many zeros are there? You would have to count them all. Is this number smaller or greater than: 0.0000000000001?
因为我们经常遇到数字,我们希望能够以最简洁的方式表达它们。把一个小数字写为:0.000000000001是相当麻烦的。有多少个零?你得把它们都算出来。这个数字是小于还是大于0.0000000000001?
We can instead use powers of 10 to express any number as a product of a digit term and an exponential term. For example,
我们可以用10的幂表示任何数字,它是一个数字项和一个指数项的乘积。例如,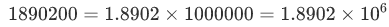
Because 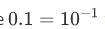 we can also compress subunitary numbers:
we can also compress subunitary numbers: 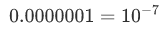 . This notation is not only more concise, but also much faster and error-proof in manipulations. For example:
. This notation is not only more concise, but also much faster and error-proof in manipulations. For example:
因为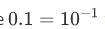 我们还可以压缩次幂数
我们还可以压缩次幂数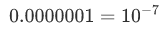 。这个符号不仅更简洁,而且操作速度更快,更可靠。例如:
。这个符号不仅更简洁,而且操作速度更快,更可靠。例如:
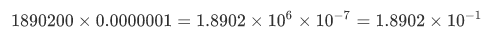
Unit Prefixes
单位前缀
| 前缀 | 符号 | 十进制 | |
|---|---|---|---|
| Tera | |||
| Giga | |||
| Mega | |||
| Kilo | |||
| Mili | |||
| Micro | |||
| Nano | |||
| Pico |


