The Light Clock

光钟

In this supplement we are going to derivethe formula for the time dilation using the thought model of a light clock. Themathematical derivation uses only Pythagoras's theorem and some basic algebraicmanipulations. These steps are important to form an idea of where themysterious γ factor is coming from.

在这个补充中，我们将利用钟的思维模型推导出时间膨胀的公式。数学推导利用毕达哥拉斯定理和一些基本的代数运算。这些步骤对于形成神秘的γ因子从何而来是很重要的。

The Light Clock

光时钟

In the previous videos we have compared arest and a moving light clock to explain the dilation of time. The light clockitself is formed by two mirrors and a ray of light (or light particles)  that bounces between them (see fig. 1).Without changing anything about this clock, we start moving it with a constantvelocity v (see fig. 2).

在前面的视频中，我们比较了休息和移动的光时钟来解释时间的膨胀。光时钟本身是由两个反射镜和一束光线（或轻粒子）在它们之间反弹（见图1）形成的。在不改变这个时钟的任何情况下，我们开始以恒定的速度v移动它（参见图2）。

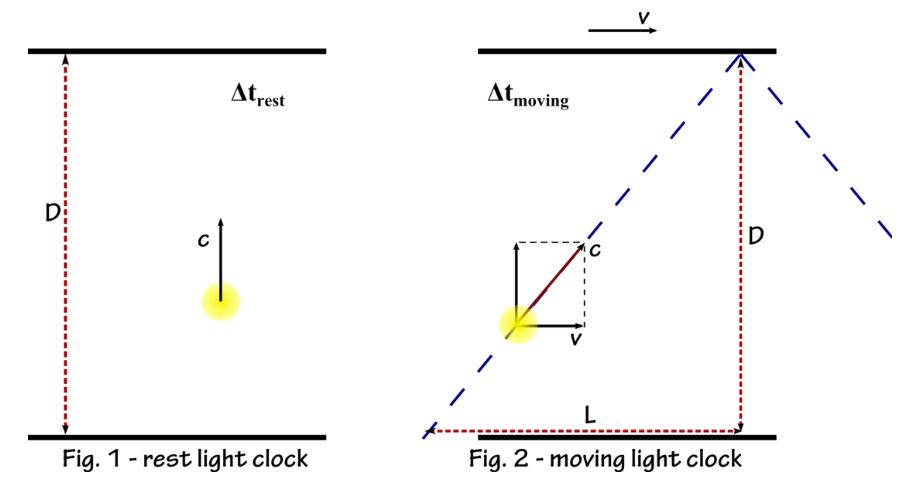
The clock mechanism always emits light rayswith velocity c perpendicular to the mirror, but now we also need to take intoaccount the motion of the clock itself. In regular classical mechanics, anobserver at rest would vectorially add up the two velocities to get theresultant c→+v→.

时钟机构总是以垂直于镜子的速度C发出光线，但现在我们还需要考虑到时钟本身的运动。在常规的经典力学，静止的观察者将矢量相加的两速度获得由此产生的c→+v→.

However, from Einstein's second principlewe know that light always travel at a constant speed (c=300 000 km/s in vacuum)independently of the observer or the light source. So for the observer at rest,the light ray in the moving clock moves with velocity c→ along the diagonal path.

然而，从爱因斯坦的第二原理，我们知道光总是以恒定的速度（真空中的C = 300 000公里/秒）独立于观察者或光源。因此，在休息观察，运动中的时钟移动速度C→沿对角线路径的光线。

Now we have everything in place to get thefamous time dilation formula. For the rest light clock, a unit of timecorresponds to the interval between two clicks:

现在我们已经掌握了著名的时间膨胀公式。其余的光时钟，一个单位时间对应间隔点击：

For the moving light clock a unit of timecorresponds to the total distance covered by light divided by its speed.Because light travels on the hypotenuse of the right triangle, we can usePythagoras's theorem to write this distance as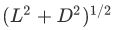. Then a unit of time on the movingclock will be:

对于移动光时钟，时间单位对应于由其速度除以光所覆盖的总距离。因为光速在直角三角形的斜边，我们可以用毕达哥拉斯定理来写这个距离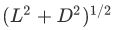。然后移动时钟上的时间单位是：

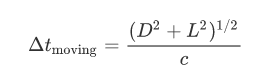
On the horizontal direction light needs tocover the length L which corresponds to the distance over which the mirror hasmoved. Because the mirror moves with velocity v,

在水平方向上，光线需要覆盖与镜子移动距离相对应的长度L。因为镜子以速度v移动，

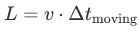
Now we replace L and D above and get:

现在我们在上面替换L和D并得到：

This is the math! We encourage you to tryit out yourself especially if it looks intimidating.

这是数学！我们鼓励你自己去尝试，尤其是当它看起来很吓人的时候。              

Often this is re-written as:

通常这是重写为

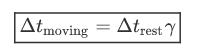
where γ is the Lorentz factor (we alreadyencountered it for the length contraction in the first lecture), and is definedas

其中，γ是洛伦兹因子（我们在第一堂课中已经找到了长度收缩），并定义为

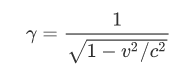
We'll discuss this result in the followingunit.

我们将在下面的单元中讨论这个结果。