Dimensional Analysis

量纲分析  

Energy

能量

In our previous discussions of kinematics(the study of the motion of particles) we only encountered two fundamentalphysical quantities: space and time. However, if we want to talk about theenergy of a particle, we also need to consider the amount of matter that ismoving, i.e. the mass of the particle (m). We will call M the dimension of thisthird fundamental quantity:

在我们以前的运动学讨论（粒子运动的研究）中，我们只遇到了两个基本物理量：空间和时间。然而，如果我们想讨论一个粒子的能量，我们也需要考虑移动的物质的量，即粒子的质量（m）。我们称M为这第三个基本量的维数：

 [m]=M

The dimensions of all the physicsquantities you will ever encounter in mechanics can be described in terms of L,T, M.

你在力学中遇到的所有物理量的维度可以用L，T，M.来描述。

The Boltzmann Constant

玻尔兹曼常数            

Thermodynamics and the molecular theory ofheat have their own fundamental physical quantity - temperature, T. However,because we have used T to refer to the dimension of time, we will use the Greekletter "theta", Θ, to refer to the dimensions of temperature:

 热力学和热分子理论有自己的基本的物理量-温度，但是，因为我们已经用T指时间维度，我们将使用希腊字母“θ”，参考温度的维度：

[T]=Θ

Caution: In the case of the quantity oftime t we have defined its dimension to be T, and we wrote: [t]=T. This iswhere the bracket notation comes in handy because it keeps a clear distinctionbetween the quantities and the dimensions.

注意：在时间t的情况下，我们定义了它的维数为t，我们写了：[t]=T。这是括号记号的用法，因为它在数量和维度之间有一个清晰的区分。

The success of the molecular theory of heatwas based on its ability of relating microscopic (connected to the motion ofmolecules) and macroscopic variables (describing the whole system of particlessuch as temperature or pressure). One such expression that bridged the microscopicand macroscopic was:

分子热理论的成功基于它的微观关联（与分子运动相联系）和宏观变量（描述粒子的整个系统，如温度或压力）。一种表达了微观和宏观的表达式：

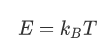
Here one relates the kinetic energy ofmolecules (depending only on their mass and velocity) to the temperature of thegas - i.e. the whole system of molecules. (This is not quite the preciseexpression of the energy. There are a few extra dimensionless factors that needto be included to account for the different types of motion that a molecule canhave. For simplicity, we have dropped the extra numerical factors. For thepurpose of this course, this will not make a difference.)

在这里，我们把分子的动能（只取决于它们的质量和速度）与气体的温度（即整个分子系统）联系起来。（这不是能量的精确表达式。）。有几个额外的无量纲因素需要包括在内，以说明不同类型的运动，一个分子可以有动能。为了简单起见，我们已经放弃了额外的数值因素。为了这个课程的目的，这不会有任何影响。）

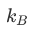 is called the Boltzmann constant (afterLudwig Boltzmann) and it is a fundamental constant of physics, similar to thespeed of light.

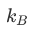被称为玻尔兹曼常数（在路德维希·玻尔兹曼之后），它是物理学的基本常数，类似于光的速度。

The Planck Constant

普朗克常量

In the lesson about the PhotoelectricEffect we have encountered another formula for energy:

在关于光电效应的教训中，我们遇到了另一种能量公式：

E=hv

where v is the frequency of a wave, and Ethe energy of the wave. h is the Planck constant, also a fundamental constantof physics.

其中v是波的频率，E是波的能量。h是普朗克常数，也是物理学的基本常数。             

The meaning of this formula is very similarto 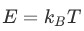 as it relates a microscopic and a macroscopic description of the samephenomena. If in the case of the Brownian Effect, the temperature is themacroscopic quantity characterizing the system, in the case of thePhotoelectric Effect, the frequency of the waves are the equivalent macroscopicquantity. As in the case of temperature, the wave frequency is an observablequantity and it can easily be measured.

此公式的含义是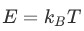：非常相似，因为它涉及微观和宏观描述相同的现象。如果在布朗效应的情况下，温度是表征系统的宏观量，在光电效应的情况下，波的频率是等效的宏观量。在温度的情况下，波频率是可观察到的量，并且可以很容易地测量。

In both cases E refers to the kineticenergy of some unobservable (at the time) particles: molecules in the case ofthe Brownian Effect, and photons in the case of the Photoelectric Effect.

在这两种情况下，E指的是一些不可观测的动能（当时）颗粒：在布朗的影响的情况下的分子，在光电效应的光子。

If we also include Einstein's famousrelation between energy and mass, we have three, structurally similar formulas:

如果我们还包括爱因斯坦著名的能量和质量的关系，我们有三个，结构相似的公式：

E=mc² (Einstein)

E=hν (Planck)

E=k_BT (Boltzmann)

There are subtle differences between theseexpressions, and the way he have interpreted them has changed throughout time.It is enough to remember that in his Photoelectric Effect Paper, Einsteinborrowed Planck's equation and applied it to light - an unintended applicationfor Planck这些表达方式之间有细微的差别，他解释它们的方式在整个时间里都发生了变化。记住，在他的光电效果文件中，爱因斯坦借用了普朗克的公式并应用于光—这是普朗克的一个意外应用。             .

In all three cases one connects an energyto a macroscopic quantity (mass, frequency or temperature) using a fundamentalconstant. These are not ad-hoc or empirical formulas, but they express afundamental physical connection.

在这三种情况下，一种能量都用基本常数将宏观量（质量、频率或温度）连接起来。这些不是特设的或经验公式，但它们表达了基本的物理联系。