离散数学

段冬燕 李静

目录

  • 1 绪言
    • 1.1 离散数学概述
  • 2 数理逻辑
    • 2.1 命题逻辑
      • 2.1.1 命题与命题联结词、命题公式
      • 2.1.2 公式分类与等值演算
      • 2.1.3 基本蕴涵式及蕴涵推理
      • 2.1.4 范式
      • 2.1.5 其他网络资源
        • 2.1.5.1 网络资源：命题逻辑（一）
        • 2.1.5.2 网络资源：命题逻辑（二）
        • 2.1.5.3 网络资源：命题逻辑（三）
    • 2.2 谓词逻辑
      • 2.2.1 谓词和量词
      • 2.2.2 谓词公式及分类
      • 2.2.3 自然语句形式化
      • 2.2.4 谓词逻辑的等值演算
      • 2.2.5 前束范式
      • 2.2.6 谓词逻辑的推理
  • 3 集合论
    • 3.1 集合的基本概念
    • 3.2 集合运算
    • 3.3 笛卡儿乘积与关系基本概念
    • 3.4 关系的运算
    • 3.5 关系的重要性质
      • 3.5.1 关系重要性质测验
    • 3.6 关系的闭包运算
    • 3.7 次序关系
      • 3.7.1 次序关系预习检测
    • 3.8 等价关系
    • 3.9 函数
    • 3.10 网络资源
      • 3.10.1 网络资源：二元关系和函数（二）
      • 3.10.2 网络资源：二元关系和函数（三）
      • 3.10.3 网络资源：二元关系和函数（四）
  • 4 图论
    • 4.1 图的基本概念
    • 4.2 通路、回路与连通性+欧拉图
    • 4.3 图的矩阵表示法与离散建模实例
    • 4.4 常用图——树
    • 4.5 网络资源
      • 4.5.1 网络资源：图的基本概念（一）
      • 4.5.2 网络资源：图的基本概念（二）
      • 4.5.3 网络资源：图的基本概念（三）
      • 4.5.4 网络资源：一些特殊的图（二）（选读）
      • 4.5.5 网络资源：一些特殊的图（一） (选读)
  • 5 代数系统
    • 5.1 代数系统的基本概念+一些基本性质
    • 5.2 同构与同态
    • 5.3 群的基本概念
    • 5.4 几个特殊的群
    • 5.5 网络资源
      • 5.5.1 网络资源：代数系统的一般性质（一）
      • 5.5.2 网络资源：代数系统的一般性质（二）
      • 5.5.3 网络资源：几个典型的代数系统（一）
      • 5.5.4 网络资源：几个典型的代数系统（二）
图的矩阵表示法与离散建模实例
  • 1 学习目标、学习任务单
  • 2 学习内容
  • 3 拓展提高

学习目标：

1. 掌握图的邻接矩阵及有向图的可达性矩阵的求法

2. 根据邻接矩阵求对应图的数量特征

3. 利用矩阵计算判断图的连通性

学习任务单：

1. 预习学习通上“8.3  图的矩阵表示法”的相关视频、课件、讲义，电子版教材P127-P133。

2. 预习提示：本次课程是本章的重点，也是本课程的重点，涉及到的矩阵计算方法如果没有掌握的话，大家在课前一定要再复习一下相关知识点。矩阵计算的过程比较繁琐，大家一定要自己动手去写一下，计算时一定要细心、耐心，否则很容易出错。

3. 预习后回答以下问题：

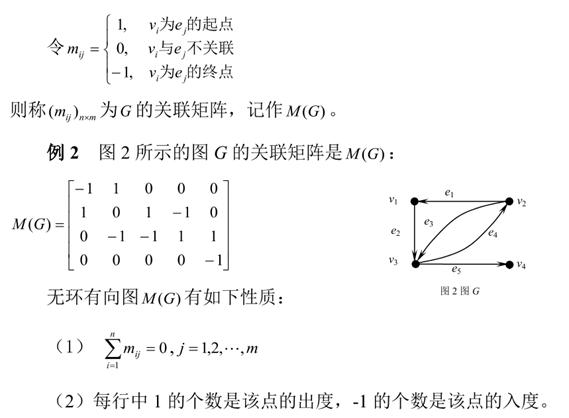
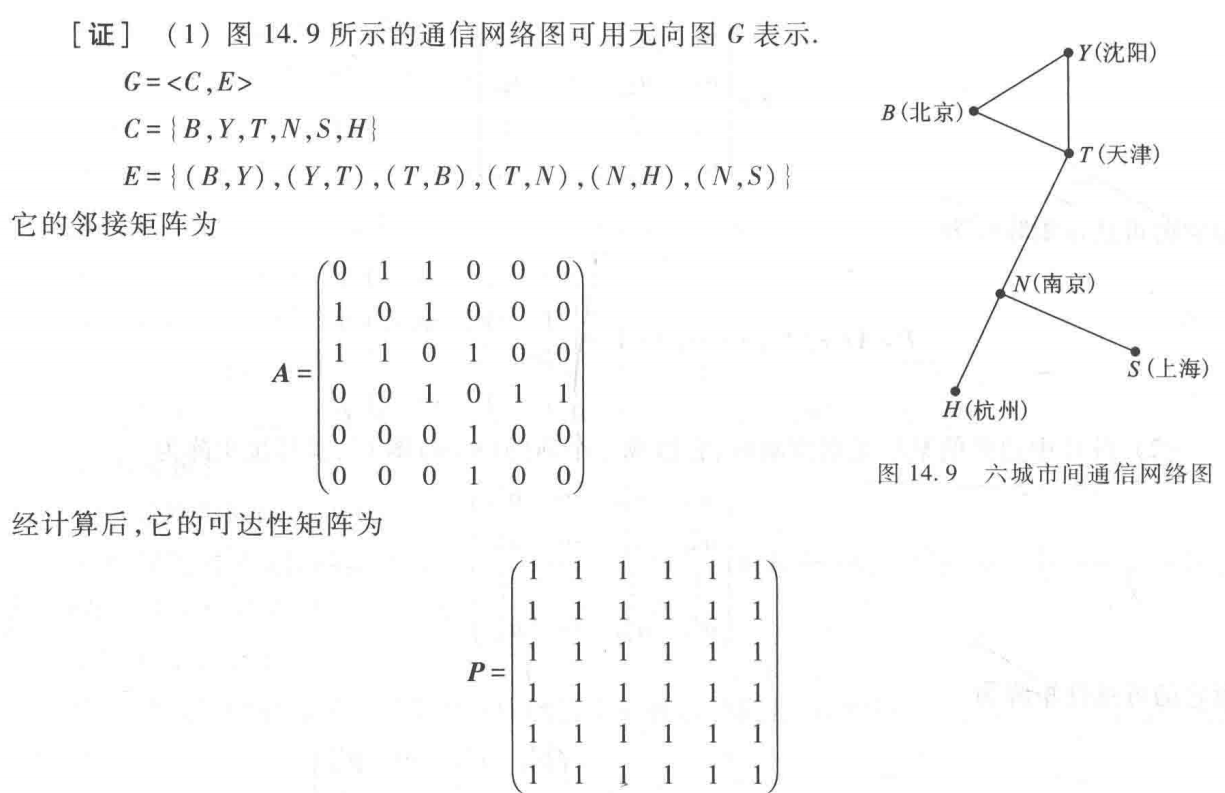
(1) 邻接矩阵刻画的是点与点的关系还是点与边的关系？如何构造有向图的邻接矩阵？矩阵乘法的规则是什么？

(2) 如何求从vi到vj的长度为n的通路数目？如何构造图的可达性矩阵？

(3) 如何构造无向图的邻接矩阵？

(4) 如何利用矩阵计算判断一个有向图的强连通性和单向连通性？