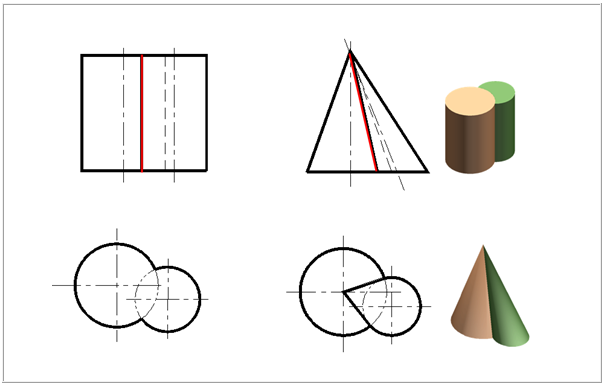
组合体的相贯与截交
在生产实际中经常会遇到一些截交和相贯的问题,拉杆接头上的截交线(如下图(a)所示)和三通上的相贯线(如下图(b)所示),因此必须研究求作截交线和相贯线的一般方法。


(a) (b)
组合体上的截交线
截交线是截平面与组合体表面的共有线,所以求截交线的实质,就是求出截平面与组合体表面的一系列共有点的集合。
求同轴复合回转体的截交线的方法:
→ 首先要分析该立体是由哪些基本体所组成的。
→ 再分析截平面与每个被截的基本体的相对位置、截交线的形状和投影特征。
→ 然后逐个画出基本体的截交线,围成封闭的平面图形。
例: 求拉杆接头的主、左视图。
→ 分析:
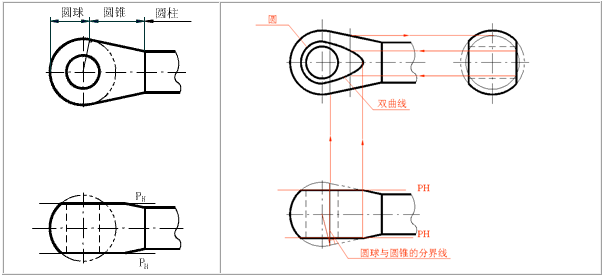
该组合体( 拉杆接头 )由同轴的圆柱、圆锥和圆球三部分构成。头部被正平面P前、后 对称地各切去一块,在前、后表面上各产生一条封闭的平面曲线。
从俯视图中可以看出,截平面P和圆柱不相交,P平面和圆球的截交线是圆,P平面和圆锥的截交线为双曲线。由于截平面为正平面,所以截交线的 V 面投影反映其实形,H面、W面投影积聚成直线段。
→ 作图:(如下图所示)
1 、找到圆球与圆锥的分界线, 然后分别求出这两段截交线,两段截交线的结合点必在分界线上。
2
、找到双曲线的特殊点(顶点)。
3 、找到双曲线的一般点。
组合体上的相贯线
两个基本体的表面彼此相交的组合体,称为相贯体,其表面交线称为相贯线。
由于彼此相贯的两基本形体的形状、大小及相互位置不同,相贯线的形状也就不同。任何相贯线都具有以下两个基本性质:
• 共有性——相贯线是相交两基本形体表面的共有线,也是它们表面的分界线。
• 封闭性——由于基本形体有一定的范围,所以相贯线一般是封闭的。
求相贯线的实质问题,就是在两个基本形体的表面上找出若干个共有点。
求相贯线的方法:
→利用积聚性表面取点法
→辅助平面法
→辅助球面法
求相贯线的具体作图步骤:
→先找特殊点。
→再找一般点。
→判断可见性。
→光滑连接。
•表面取点法求相贯线
1)用表面取点法求相贯线。
例:求两圆柱正交(即两圆柱的轴线垂直相交)的相贯线。
→分析:
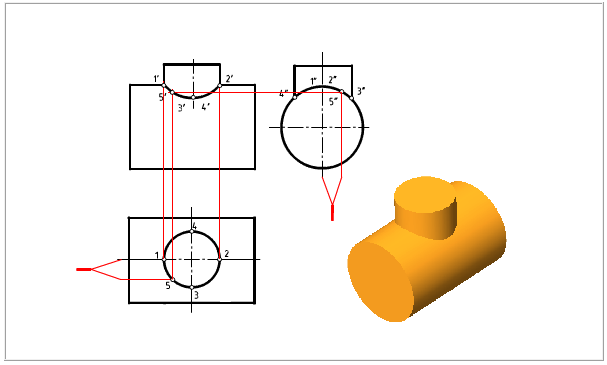
因为两圆柱的轴线分别垂直于H面和W面, 所以利用积聚性可以在图上直接得到相贯线的H面投影为圆。相贯线的W面投影为一段圆弧。相贯线的V面投影需要由作图求出。
→作图:
求作相贯线的V面投影时,应先求交线上的特殊点,从主视图中可知,两圆柱外形素线的交点Ⅰ和Ⅱ,就是交线上的最高点,其V面投影为1′和2′。从左视图可知,小圆柱的外形素线与大圆柱表面的交点Ⅲ和Ⅳ是交线的最低点,其W面投影为3"和4"。已知3"、4"和3、4即可求得3′、4′。
为了使交线的投影画得比较准确,再求适当数量的一般点如 5 ′……等。然后用曲线板把各点光滑地连接起来,即得所求交线的V面投影,如下图所示。
2)、两圆柱正交的形式
常见的形式有三种:
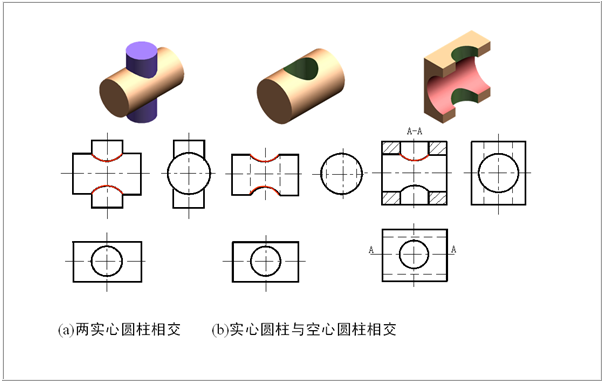
两实心圆柱相交;实心圆柱与空心圆柱相交;两个空心圆柱相交,如下图所示。
3)、相贯线形状的变化
两圆柱直径比值的改变,会引起交线的性质、弯曲程度和走向发生变化,相贯线的变化趋势如下图所示。
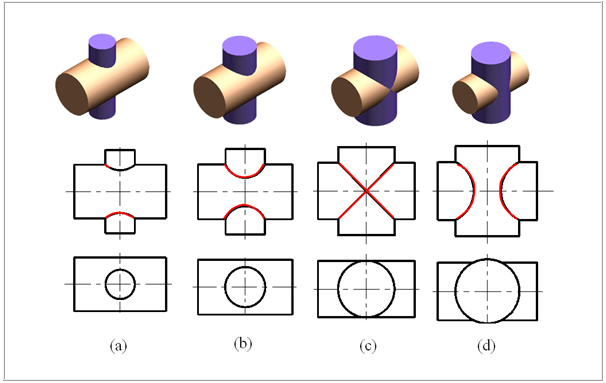
(a) 水平圆柱与直立圆柱的直径相差较大。
(b) 直立圆柱的直径逐渐增大,相贯线弯曲增大。
(c) 两圆柱的直径相等,相贯线为椭圆,V面投影为两条直线。
(d)
直立圆柱直径大于水平圆柱,相贯线改变弯曲方向。
显然我们可得出如下结论:两圆柱正交时,其相贯线总是凸向大圆柱的轴线 。
• 用辅助平面法求相贯线
→辅助平面法——是利用辅助平面求两基本形体表面共有点的方法。设想在适当的位置,用一个辅助平面同时截割相贯的两基本体,使两基本形体表面上都产生截交线,找出两截交线的交点,即是相贯线上的点。这些点既在两曲面立体的表面上,又在辅助平面上,因而是三个面(一个平面和两个曲面)的共有点。这就是三面共点原理。
根据以上原理,在投影图中,可按如下步骤求共有点的投影:
1) 作出假想的辅助平面(用迹线表示),与两已知曲面相交 ;
2) 作出辅助平面与两已知曲面的截交线;
3) 两截交线的交点,即为两曲面共同点。
3、相贯线的特殊情况
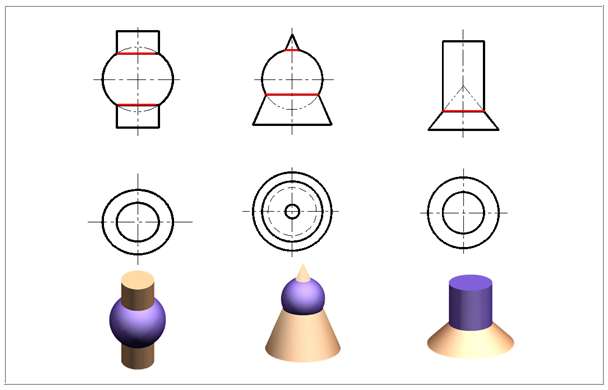
(1)当两个回转体具有公共轴线时,相贯线为圆。当轴线垂直于水平面时,该圆的正面投影为一直线段,水平投影为圆的实形,如下图所示。
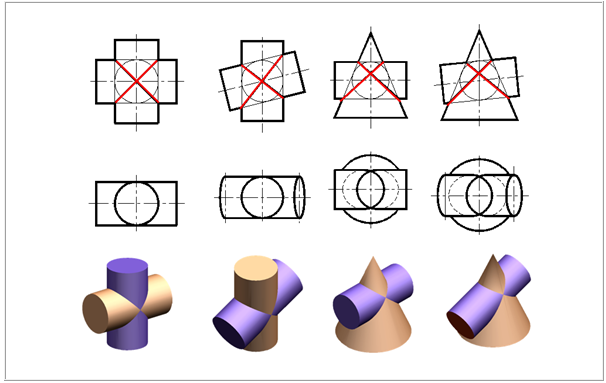
(2)当圆柱与圆柱、圆柱与圆锥相贯,公切于一圆球时, 相贯线为平面曲线,若曲线所在平面与投影面垂直时,则在该投影面上的投影为一直线段,如下图所示。
(3)相贯线是直线
当两圆柱的轴线平行或两圆锥共顶时,相贯线是直线,如下图所示。