2．场模型

对于模拟具有一定空间内连续分布特点的现象来说，基于场的观点是合适的。例如，空气中污染物的集中程度、地表的温度、土壤的湿度水平以及空气与水的流动速度和方向。根据应用的不同，场可以表现为二维或三维。一个二维场就是在二维空间中任何已知的地点上，都有一个表现这一现象的值；而一个三维场就是在三维空间中对于任何位置来说都有一个值。一些现象，诸如空气污染物在空间中本质上讲是三维的，但是许多情况下可以由一个二维场来表示。

场模型可以表示为如下的数学公式：

z : sà z ( s )

上式中，z为可度量的函数，s表示空间中的位置，因此该式表示了从空间域（甚至包括时间坐标）到某个值域的映射。表3-1给出了地理研究中一些常模型的例子[A. Vckovski]。

2．1场的特征

场经常被视为由一系列等值线组成，一个等值线就是地面上所有具有相同属性值的点的有序集合。

2．1．1空间结构特征和属性域

在实际应用中，“空间”经常是指可以进行长度和角度测量的欧几里德空间。空间结构可以是规则的或不规则的，但空间结构的分辨率和位置误差则十分重要，它们应当与空间结构设计所支持的数据类型和分析相适应。属性域的数值可以包含以下几种类型：名称、序数、间隔和比率。属性域的另一个特征是支持空值，如果值未知或不确定则赋予空值。

2．1．2连续的、可微的、离散的

如果空间域函数连续的话，空间域也就是连续的，即随着空间位置的微小变化，其属性值也将发生微小变化，不会出现像数字高程模型中的悬崖那样的突变值。只有在空间结构和属性域中恰当地定义了“微小变化”，“连续”的意义才确切；

当空间结构是二维（或更多维）时，坡度——或者称为变化率——不仅取决于特殊的位置，而且取决于位置所在区域的方向分布（图3-2）。连续与可微分两个概念之间有逻辑关系，每个可微函数一定是连续的，但连续函数不一定可微。

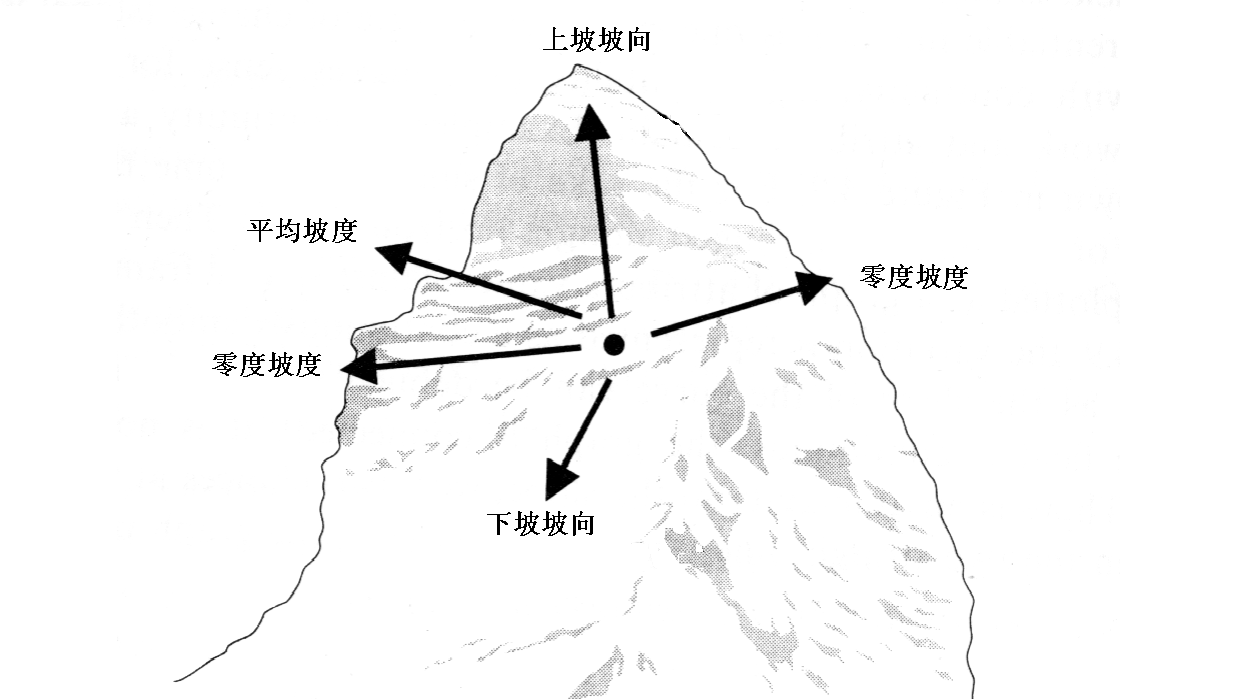
图3-2：某点的坡度取决于位置所在区域的各方向上的可微性

如果空间域函数是可微分的，空间域就是可微分的；行政区划的边界变化是离散的一个例子，如果目前测得的边界位于A，而去年这时边界位于B，但这并不表明6个月前边界将位于BA之间的中心，边界具有不连续跃变。

2．1．3与方向无关的和与方向有关的（各向同性和各向异性）

空间场内部的各种性质是否随方向的变化而发生变化，是空间场的一个重要特征。如果一个场中的所有性质都与方向无关，则称之为各向同性场(Isotropic Field)。例如旅行时间，假如从某一个点旅行到另一个点所耗时间只与这两点之间的欧氏几何距离成正比，则从一个固定点出发，旅行一定时间所能到达的点必然是一个等时圆，如图3-3-(a)所示。如果某一点处有一条高速通道，则利用与不利用高速通道所产生的旅行时间是不同的，见图3-3-(b)。等时线已标明在图中，图中的双曲线是利用与不利用高速通道的分界线。本例中的旅行时间与目标点与起点的方位有关，这个场称为各向异性场（Anisotropic Field）。

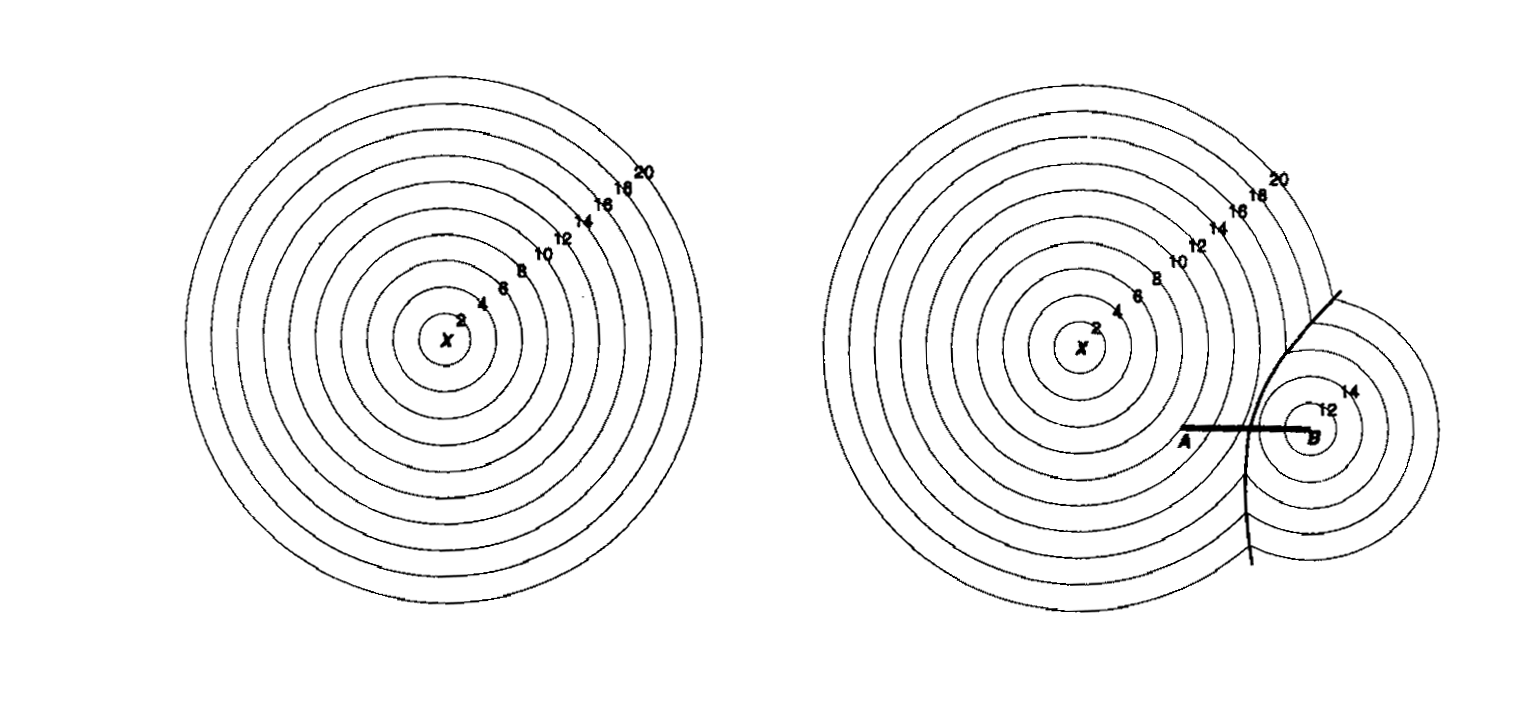
                                                (a)                                                                 (b)

图3-3：在各向同性与各向异性场中的旅行时间面

2．1．4空间自相关

空间自相关是空间场中的数值聚集程度的一种量度。距离近的事物之间的联系性强于距离远的事物之间的联系性。如果一个空间场中的类似的数值有聚集的倾向，则该空间场就表现出很强的正空间自相关；如果类似的属性值在空间上有相互排斥的倾向，则表现为负空间自相关（图3-4）。因此空间自相关描述了某一位置上的属性值与相邻位置上的属性值之间的关系。

图3-4：强空间正负自相关模式

2．2栅格数据模型

栅格数据模型是基于连续铺盖的，它是将连续空间离散化，即用二维铺盖或划分覆盖整个连续空间；铺盖可以分为规则的和不规则^*的，后者可当做拓扑多边形处理，如社会经济分区、城市街区；铺盖的特征参数有尺寸、形状、方位和间距。对同一现象，也可能有若干不同尺度、不同聚分性（Aggregation or Subdivisions）的铺盖。在边数从3到N的规则铺盖（Regular Tesselations）中，方格、三角形和六角形是空间数据处理中最常用的。三角形是最基本的不可再分的单元，根据角度和边长的不同，可以取不同的形状，方格、三角形和六角形可完整地铺满一个平面（图3-5）。

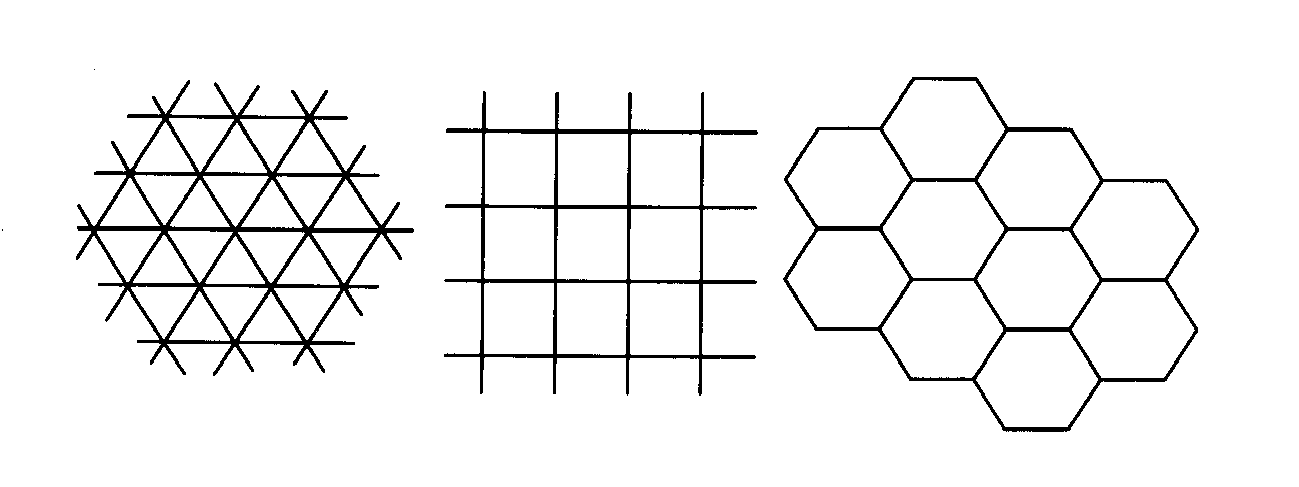
图3-5：三角形、方格和六角形划分

基于栅格的空间模型把空间看作像元（Pixel）的划分（Tessellation），每个像元都与分类或者标识所包含的现象的一个记录有关。像元与“栅格”两者都是来自图像处理的内容，其中单个的图像可以通过扫描每个栅格产生。GIS中栅格数据经常是来自人工和卫星遥感扫描设备中，以及用于数字化文件的设备中。采用栅格模型的信息系统，通常应用了前面所述的分层的方法。在每个图层中栅格像元记录了特殊的现象的存在。每个像元的值表明了在已知类中现象的分类情况（图3-6）。

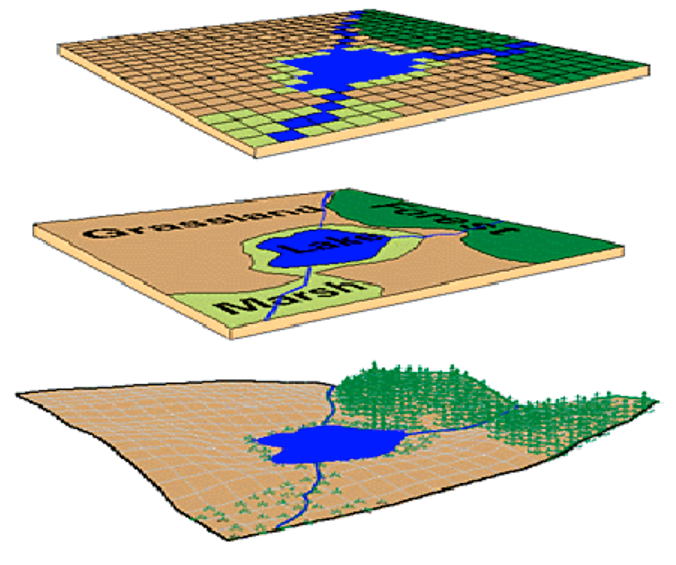
图3-6：栅格数据模型

由于像元具有固定的尺寸和位置，所以栅格趋向于表现在一个“栅格块”中的自然及人工现象。因此分类之间的界限被迫采用沿着栅格像元的边界线。一个栅格图层中每个像元通常被分为一个单一的类型。这可能造成对现象的分布的误解，其程度则取决与所研究的相关的像元的大小。如果像元针对特征而言是非常小的，栅格可以是一个来表现自然现象的边界随机分布的特别有效的方式，该现象趋于逐渐地彼此结合，而不是简单地划分。如果每个像元限定为一个类，栅格模型就不能充分地表现一些自然现象的转换属性。除非抽样被降低到一个微观的水平，否则许多数据类事实上都是混合类。模糊的特征通过混合像元，在一个栅格内可以被有效地表达，其中组成分类通过像元所有组成度量的或者预测的百分比来表示。尽管如此，也应该强调一个栅格的像元仅仅被赋予一个单一的值。

为了GIS数据处理，栅格模型的一个重要的特征就是每个栅格中的像元的位置被预先确定，所以很容易进行重叠运算以比较不同图层中所存储的特征。由于像元位置是预先确定的，且是相同的，在一个具体的应用的不同的图层中，每个属性可以从逻辑上或者从算法上与其它图层中的像元的属性相结合以便产生相应的重叠中一个的属性值。其不同于基于图层的矢量模型之处，在于图层中的面单元彼此是独立的，直接地比较图层必须作进一步处理以识别重叠的属性。