2．空间数据录入后的处理

2．1图形坐标变换

在地图录入完毕后，经常需要进行投影变换，得到经纬度参照系下的地图。对各种投影进行坐标变换的原因主要是输入时地图是一种投影，而输出的地图产物是另外一种投影。进行投影变换有两种方式，一种是利用多项式拟合，类似于图像几何纠正；另一种是直接应用投影变换公式进行变换。

2．1．2基本坐标变换

在投影变换过程中，有以下三种基本的操作：平移、旋转和缩放。

1）平移

平移是将图形的一部分或者整体移动到笛卡尔坐标系中另外的位置(图6-11-a)，其变换公式如下：

X’=X+T_x

Y’=Y+T_y

2）缩放

缩放操作可以用于输出大小不同的图形（图6-11-b），其公式为：

X’=XS_x

Y’=YS_y

3）旋转

在地图投影变换中，经常要应用旋转操作（图6-11-c），实现旋转操作要用到三角函数，假定顺时针旋转角度为θ，其公式为^*：

X’=Xcosθ+Ysinθ

Y’=-Xsinθ+Ycosθ

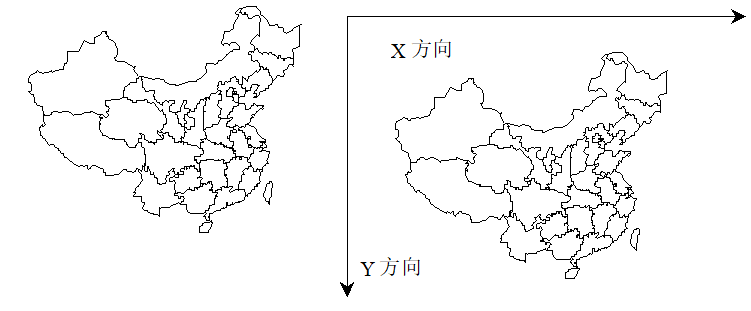
(a)平移

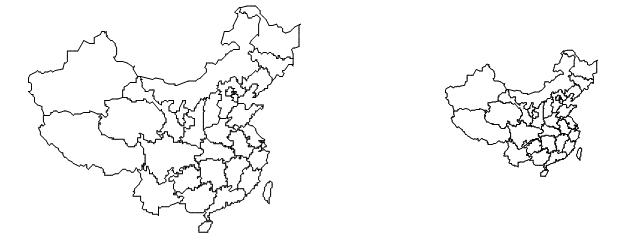
(b)缩放

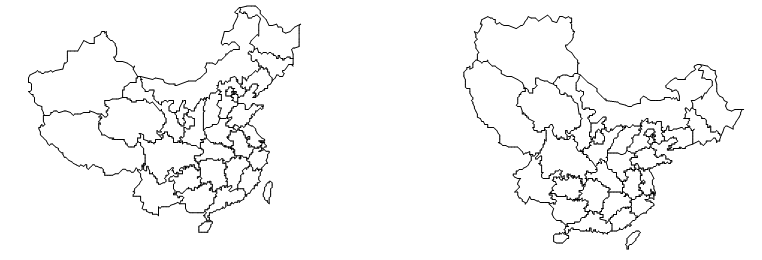
(c)图形旋转

图6-11：图形坐标变换

2．1．2仿射变换（Affine Tranformation）

如果综合考虑图形的平移、旋转和缩放，则其坐标变换式如下：

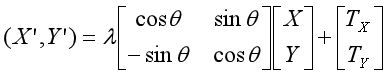
上式是一个正交变换，其更为一般的形式是：

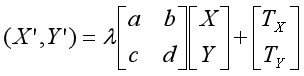
后者被称为二维的仿射变换（Affine Transformation），仿射变换在不同的方向可以有不同的压缩和扩张，可以将球变为椭球，将正方形变为平行四边形（图6-12）。

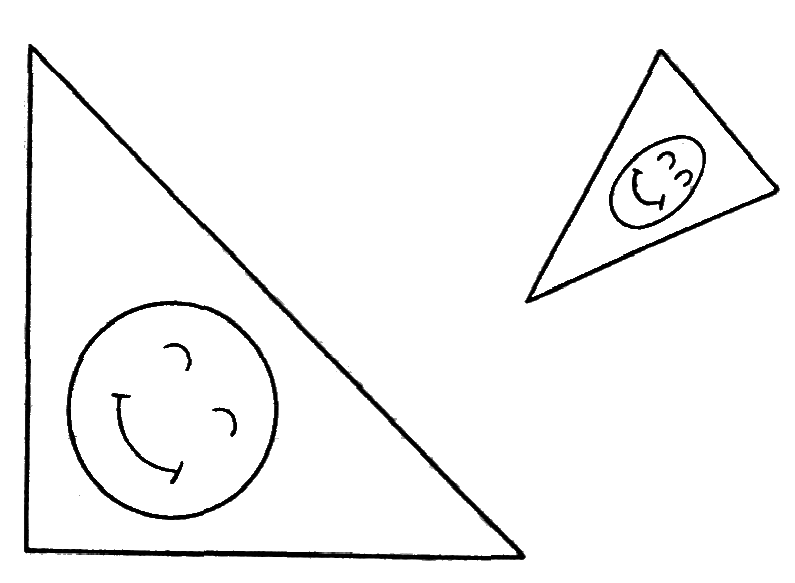
图6-12：仿射变换

2．2图形拼接

在对底图进行数字化以后，由于图幅比较大或者使用小型数字化仪时，难以将研究区域的底图以整幅的形式来完成，这是需要将整个图幅划分成几部分分别输入。在所有部分都输入完毕并进行拼接时，常常会有边界不一致的情况，需要进行边缘匹配处理（图6-13）。边缘匹配处理，类似于下面提及的悬挂节点处理，可以由计算机自动完成，或者辅助以手工半自动完成。

除了图幅尺寸的原因，在GIS实际应用中，由于经常要输入标准分幅的地形图，也需要在输入后进行拼接处理，这时，一般需要先进行投影变换，通常的做法是从地形图使用的高斯——克吕格投影转换到经纬度坐标系中，然后再进行拼接。

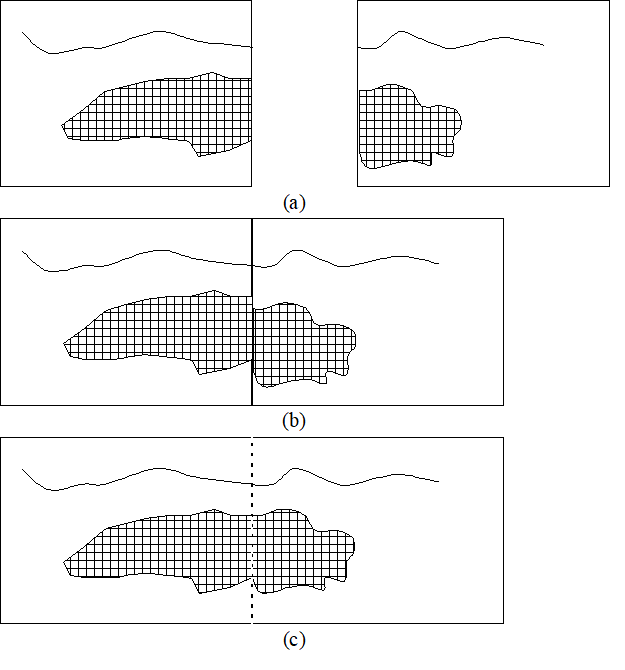
图6-13：图幅拼接

(a)拼接前；（b）拼接中的边缘不匹配；(c)调整后的拼接结果

2．3拓扑生成

在图形数字化——无论是手扶跟踪数字化还是扫描矢量化——完成后，对于大多数地图需要建立拓扑，以正确判别地物之间的拓扑关系。在GIS数据管理中，拓扑关系可以定义以下内容：

1）区域，如果多边形数据DIME数据模型，每个多边形可以用一组封闭的线^*来表示，而不需要记录封闭线上的所有点，避免两次记录相邻多边形的公共边界，这样减少了数据冗余^*。

2）邻接性，另一种可以用拓扑描述的属性是多边形之间的相互邻接性。

3）连通性，连通性是指对弧段连接的判别，连通性的建立和表现是网络分析的基础。

2．3．1图形修改

在建立拓扑关系的过程中，一些在数字化输入过程中的错误需要被改正，否则，建立的拓扑关系将不能正确地反映地物之间的关系。

由于地图数字化，特别是手扶跟踪数字化，是一件耗时、烦杂的人力劳动，在数字化过程中的错误几乎是不可避免的，造成数字化错误的具体原因包括：

1）遗漏某些实体；

2）某些实体重复录入，由于地图信息是二维分布的，并且信息量一般很大，所以要准确记录哪些实体已经录入，哪些实体尚未录入是困难的，这就容易造成重复录入和遗漏；

3）定位的不准确，数字化仪分辨率可以造成定位误差，但是人的因素是位置不准确的主要原因，如手扶跟踪数字化过程中手的抖动，两次录入之间图纸的移动都可以使位置不准确；更重要的，在手扶跟踪数字化过程中，难以实现完全精确的定位，例如在水系的录入中（图6-14），将支流的终点恰好录入在干流上基本上是不可能的（图6-14-a），更常见的是图（b）和（c）所示的两种情况。

图6-14：数字化错误——不及和过头

在数字化后的地图上，错误的具体表现形式有：

1）伪节点（Pseudo Node），伪节点使一条完整的线变成两段（图15），造成伪节点的原因常常是没有一次录入完毕一条线。

图6-15：伪节点

2）悬挂节点（Dangling Node），如果一个节点只与一条线相连接，那么该节点称为悬挂节点，悬挂节点有多边形不封闭（图6-16-a）、不及和过头（图6-14-b，图6-14-c），节点不重合（图6-16-b）等几种情形。

(a)多边形不封闭                (b)节点不重合

图6-16：悬挂节点的两种情形

3）“碎屑”多边形或“条带”多边形（Sliver Polygon）

条带多边形（图6-17）一般由于重复录入引起，由于前后两次录入同一条线的位置不可能完全一致，造成了“碎屑”多边形。另外，由于用不同比例尺的地图进行数据更新，也可能产生“碎屑”多边形。

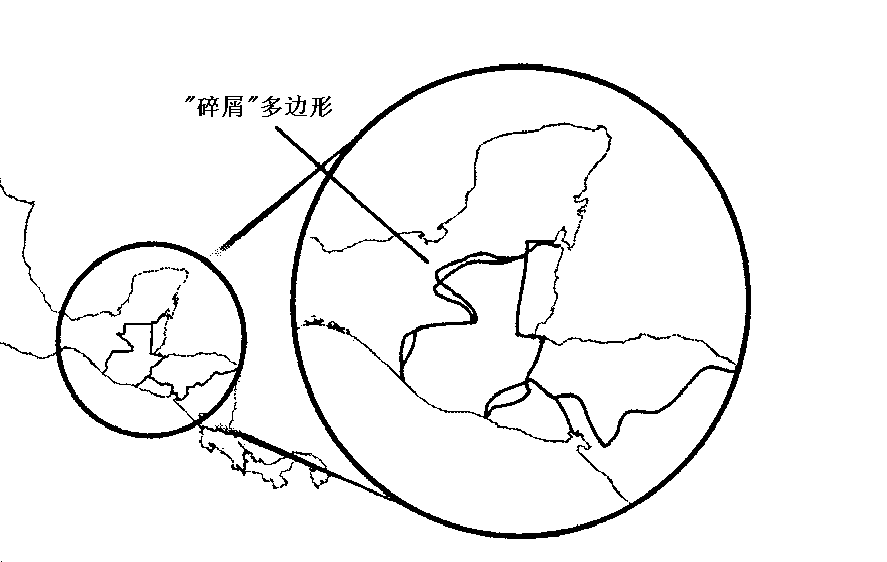
图6-17：碎屑多边形

4）不正规的多边形（Weird Polygon）

不正规的多边形（图6-18）是由于输入线时，点的次序倒置或者位置不准确引起的。在进行拓扑生成时，同样会产生“碎屑”多边形。

图6-18：不正规的多边形

上述的错误，一般会在建立拓扑的过程中发现，需要进行编辑修改。一些错误，如悬挂节点，可以在编辑的同时，由软件自动修改，通常的实现办法是设置一个“捕获距离”，当节点之间、或者节点与线之间的距离小于此数值后，即自动连接；而另外的错误需要进行手工编辑修改。

2．3．2建立拓扑关系

在图形修改完毕之后，就意味着可以建立正确的拓扑关系，拓扑关系可以由计算机自动生成，目前大多数GIS软件也都提供了完善的拓扑功能；但是在某些情况下，需要对计算机创建的拓扑关系进行手工修改，典型的例子是网络连通性。

正如拓扑的定义所描述的，建立拓扑关系时只需要关注实体之间的连接、相邻关系，而节点的位置、弧段的具体形状等非拓扑属性则不影响拓扑的建立过程。

1）多边形拓扑关系的建立

如果使用DIME或者类似的编码模型，多边形拓扑关系的表达需要描述以下实体之间的关系：

l 多边形的组成弧段；

l 弧段左右两侧的多边形，弧段两端的节点；

l 节点相连的弧段。

多边形拓扑的建立过程实际上就是确定上述的关系。具体的拓扑建立过程与数据结构有关，但是其基本原理是一致的，下面简述多边形拓扑建立过程（图6-19）。

图6-19中共有4个节点，以A、B、C、D表示；6条弧段，用数字表示；以及I、II、III三个多边形（图6-19-a）。首先定义以下概念：

l 由于弧段是有方向的，算法中将弧段A的起始节点称为首节点N_s(A)，而终止节点为尾节点N_E(A)；

l 考虑到弧段的方向性，沿弧段前进方向，将其相邻的多边形分别定义为左多边形和右多边形P_L(A)和P_R(A)。

在建立拓扑之前，首先将所有弧段的左右多边形（在实现中，可以用多边形的编码表示）都设置为空；然后对每个节点计算与其相连弧段的在连接处的角度，并进行排序（图6-19-b）（注意，这个排序是循环的）。建立拓扑的算法如下：

（1）得到第一条弧段A，并设置为当前弧段；

（2）判断P_L(A)和P_R(A)是否为空。如果都非空，转到第一步，当所有弧段处理完毕后，算法结束；

（3）如果左多边形为空，则创建一个新的多边形P，多边形的第一条弧段为当前弧段，并设置P_L(A)=P，设置搜寻起始节点为N_s(A)，搜寻当前节点为N_E(A)。如果右多边形为空，则创建一个新的多边形P，多边形的第一条弧段为当前弧段，并设置P_R(A)=P，设置搜寻起始节点N₀=N_E(A)，搜寻当前节点N_C=N_S(A)。

（4）判断N₀和N_C是否相等，如果是，则多边形所有弧段都已经找到，转到第一步。

（5）检查与当前节点相连接的、已经排列好的弧段序列，将当前弧段的下一条弧段A'作为多边形的第二条弧段。

（6）如果N_C=N_S(A')，设置P_L(A')=P，N_C=N_E(A)；如果N_C= N_E(A')，设置P_R(A')=P，N_C=N_S(A)，转到第四步。

如图6-19-c所示，如果从弧段4开始搜寻，找到节点C后，根据弧段的排序，下一条弧段是2；然后找到节点A，弧段1，整个搜寻结束，建立多边形I，其组成弧段为4、2、1。

按照这种算法，生成多边形的弧段从多边形内部看，是逆时针排列的。如果节点弧段排序为顺时针，则算法中用P_L(A)代替P_R(A)，用P_R(A)代替P_L(A)，生成的多边形弧段是顺时针排列的。

图6-19：多边形拓扑的建立过程

多边形拓扑的建立，要注意多边形带“岛”的情况，按照上述算法，对于带“岛”的多边形，或者称为环，其包含的弧段构成了多个闭合曲线，并且“岛”的弧段排序是顺时针的（图6-20）（实际上，从环状多边形内部看，它仍然是逆时针的）。

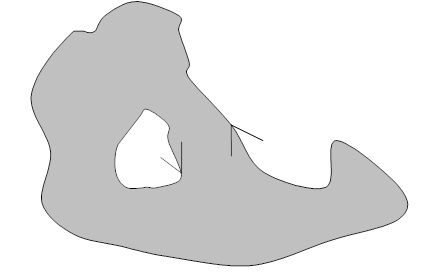
图6-20：带“岛”的多边形建立拓扑的结果。

2）网络拓扑关系的建立

在输入道路、水系、管网、通信线路等信息时，为了进行流量以及连通性分析，需要确定线实体之间的连接关系。网络拓扑关系的建立包括确定节点与连接线之间的关系，这个工作可以由计算机自动完成，但是在一些情况中，如道路交通应用中，一些道路虽然在平面上相交，但是实际上并不连通，如立交桥，这是需要手工修改，将连通的节点删除（图6-21）。

图6-21：节点的编辑，将实际不连通的线路形成的节点删除