3．DEM模型之间的相互转换

在实际应用中，DEM模型之间可以相互转换。大部分DEM数据都是规则格网DEM，但由于规则格网DEM的数据量大而不便存储，也可能由于某些分析计算需要使用TIN模型的DEM，如进行通视分析。此时需要将格网DEM转成TIN模型的DEM。反之，如果已有TIN模型的DEM数据，为满足某种应用的需要，也需要转成规则格网的DEM。

3．1不规则点集生成TIN

对于不规则分布的高程点，可以形式化地描述为平面的一个无序的点集P，点集中每个点p对应于它的高程值。将该点集转成TIN，最常用的方法是Delaunay三角剖分方法。生成TIN的关键是Delaunay三角网的产生算法，下面先对Delaunay三角网和它的偶图Voronoi图作简要的描述。

Voronoi图，又叫泰森多边形或Dirichlet图，它由一组连续多边形组成，多边形的边界是由连接两邻点线段的垂直平分线组成。N个在平面上有区别的点，按照最近邻原则划分平面：每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voronoi多边形共享一条边的相关点连接而成的三角形。Delaunay三角形的外接圆圆心是与三角形相关的Voronoi多边形的一个顶点。Delaunay三角形是Voronoi图的偶图，如图9-6所示。

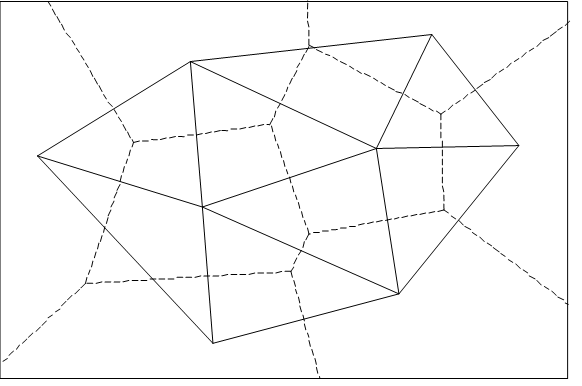
图9-6：Delaunay三角网与Voronoi图

对于给定的初始点集P，有多种三角网剖分方式，而Delaunay三角网有以下特性：

1）其Delaunay三角网是唯一的；

2）三角网的外边界构成了点集P的凸多边形“外壳”；

3）没有任何点在三角形的外接圆内部，反之，如果一个三角网满足此条件，那么它就是Delaunay三角网。

4）如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化”的三角网。

下面简要介绍Delaunay三角形产生的基本准则：

Delaunay三角形产生准则的最简明的形式是：任何一个Delaunay三角形的外接圆的内部不能包含其它任何点[Delaunay 1934]。Lawson[1972]提出了最大化最小角原则：每两个相邻的三角形构成的凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。Lawson [1977]又提出了一个局部优化过程LOP（Local Optimization Procedure）方法。如图9-7所示。先求出包含新插入点p的外接圆的三角形，这种三角形称为影响三角形（Influence Triangulation）。删除影响三角形的公共边（图b中粗线），将p与全部影响三角形的顶点连接，完成p点在原Delaunay三角形中的插入。

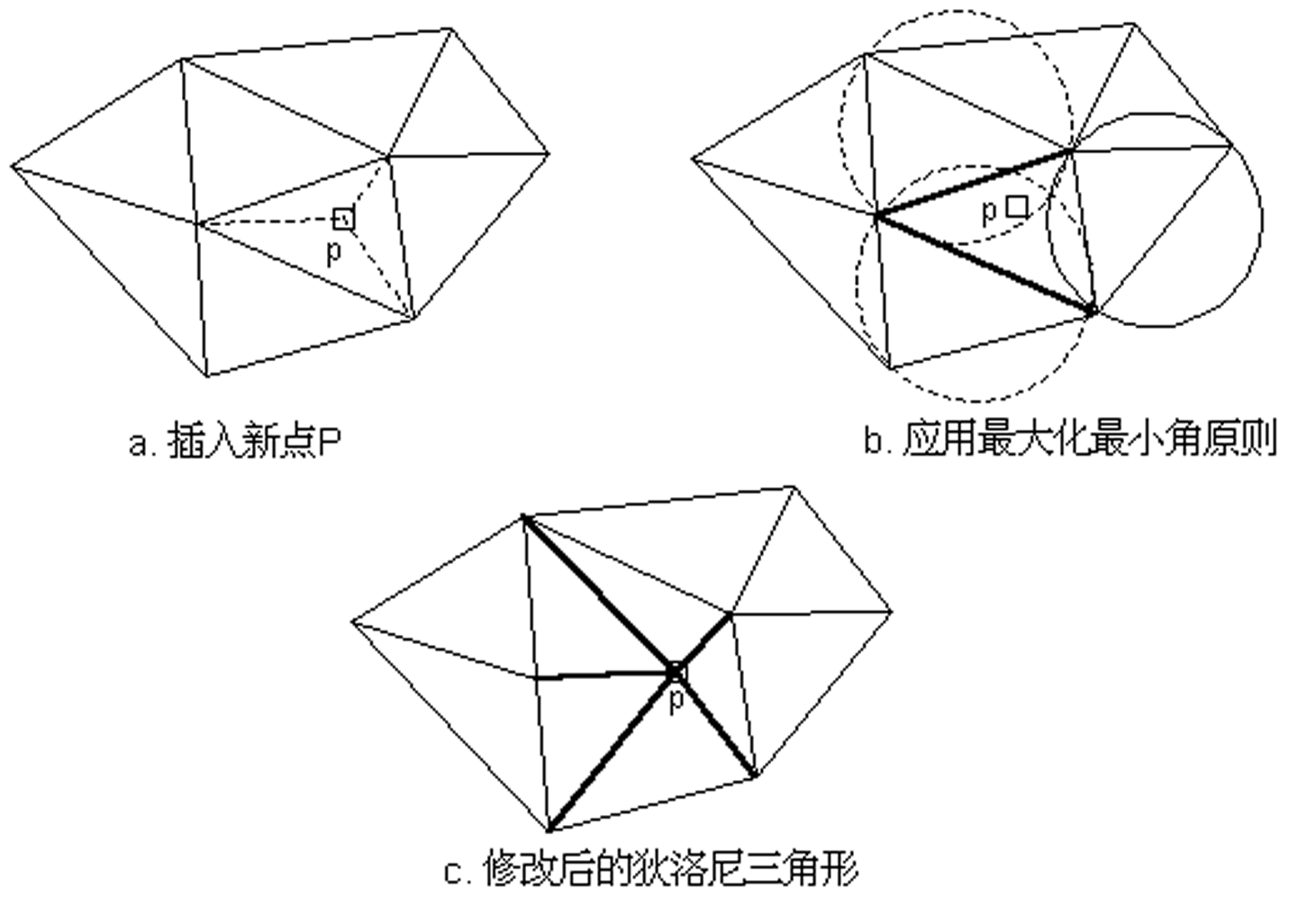
 图9-7：向Delaunay三角形中插入点

将该点集转成TIN，最常用的方法是Delaunay三角剖分方法，生成过程分两步完成：

1）利用P中点集的平面坐标产生Delaunay三角网；

2）给Delaunay三角形中的节点赋予高程值。

3．2格网DEM转成TIN

格网DEM转成TIN可以看作是一种规则分布的采样点生成TIN的特例，其目的是尽量减少TIN的顶点数目，同时尽可能多地保留地形信息，如山峰、山脊、谷底和坡度突变处。规则格网DEM可以简单地生成一个精细的规则三角网，针对它有许多算法，绝大多数算法都有两个重要的特征：

1）筛选要保留或丢弃的格网点；

2）判断停止筛选的条件。

其中两个代表性的方法算法是保留重要点法和启发丢弃法。

3．2．1保留重要点法

该方法是一种保留规则格网DEM中的重要点来构造TIN的方法[Chen、Gauvara（1987）]。它是通过比较计算格网点的重要性，保留重要的格网点。重要点（VIP，Very Important Point）是通过3*3的模板来确定的，根据八邻点的高程值决定模板中心是否为重要点。格网点的重要性是通过它的高程值与8邻点高程的内插值进行比较，当差分超过某个阈值的格网点保留下来。被保留的点作为三角网顶点生成Delaunay三角网。如图9-8所示，由3*3的模板得到中心点P和8邻点的高程值，计算中心点P到直线AE，CG，BF，DH的距离，图右图表示，再计算4个距离的平均值。如果平均值超过阈值，P点为重要点，则保留，否则去除P点。

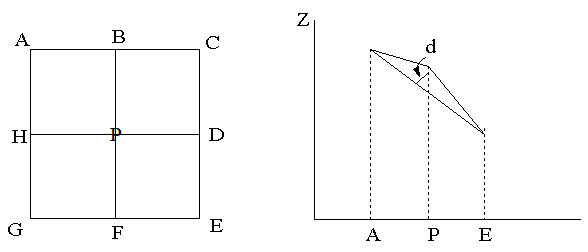
图9-8：VIP方法示意

3．2．2启发丢弃法（DH—Drop Heuristic）

该方法将重要点的选择作为一个优化问题进行处理。算法是给定一个格网DEM和转换后TIN中节点的数量限制，寻求一个TIN与规则格网DEM的最佳拟合。首先输入整个格网DEM，迭代进行计算，逐渐将那些不太重要的点删除，处理过程直到满足数量限制条件或满足一定精度为止。具体过程如下（图9-9）：

1）算法的输入是TIN，每次去掉一个节点进行迭代，得到节点越来越少的TIN。很显然，可以将格网DEM作为输入，此时所有格网点视为TIN的节点，其方法是将格网中4个节点的其中两个相对节点连接起来，这样将每个格网剖分成两个三角形。

2）取TIN的一个节点O及与其相邻的其它节点，如图9-9所示，O的邻点（称Delaunay邻接点）为A，B，C，D，使用Delaunay三角构造算法，将O的邻点进行Delaunay三角形重构，图9-9中实线所示。

3）判断该节点O位于哪个新生成的Delaunay三角形中，如图9-9为三角形BCE。计算O点的高程和过O点与三角形BCE交点O’的高程差d。若高程差d大于阈值d_e，则O点为重要点，保留，否则，可删除。d_e为阈值。

4）对TIN中所有的节点，重复进行上述判断过程。

5）直到TIN中所有的节点满足条件d>d_e，结束。

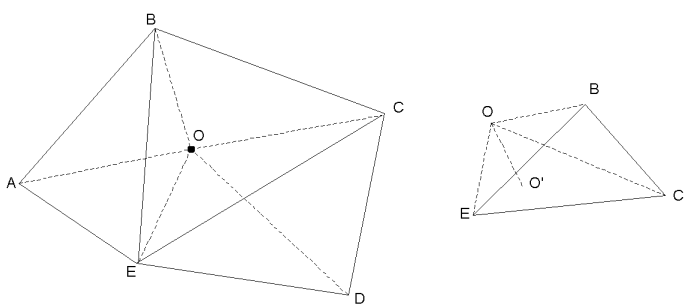
图9-9：DH方法转换格网DEM成TIN

（左图虚线为以O为中心的Delaunay三角形，实线为新生成的Delaunay三角形；

右图为高差的计算[注意：此图描述了三维空间]）

两种方法相比较[Lee，1991]，VIP方法在保留关键网格点方面（顶点、凹点）最好；DH方法在每次丢弃数据点时确保信息丢失最少，但要求计算量大。各种方法各有利弊，实际应用中根据不同的需要，如检测极值点，高效存储，最小误差，可以选择使用不同的方法。

3．3等高线转成格网DEM

表示地形的最常见的线模式是一系列描述高程曲线的等高线。由于现有地图大多数都绘有等高线，这些地图便是数字高程模型的现成数据源，可以将纸面等高线图扫描后，自动获取DEM数据。由于数字化的等高线不适合于计算坡度或制作地貌渲染图等地形分析，因此，必须要把数字化等高线转为格网高程矩阵。

使用局部插值算法，如距离倒数加权平均或克里金插值算法^*，可以将数字化等高线数据转为规则格网的DEM数据，但插值的结果往往会出现一些许多不令人满意的结果，而且数字化等高线时越小心，采样点越多，问题越严重。问题不在于计算插值权重系数的理论假设，也不在于平滑等高线是真实地形的反映的假设，而在于估计未知格网点的高程要在一个半径范围内搜索落在其中的已知点数据，再计算它的加权平均值。如果搜索到的点都具有相同的高程，那待插值点的高程也同为此高程值。结果导致在每条等高线周围的狭长区域内具有与等高线相同的高程，出现了“阶梯”地形。当低海拔平原地区等高线距离更远时，搜索到一条等高线上的数据的可能性就越大，问题更严重。以带“阶梯”地形的DEM为基础，计算坡度往往会出现不自然的条斑状分布模式（图9-10）。

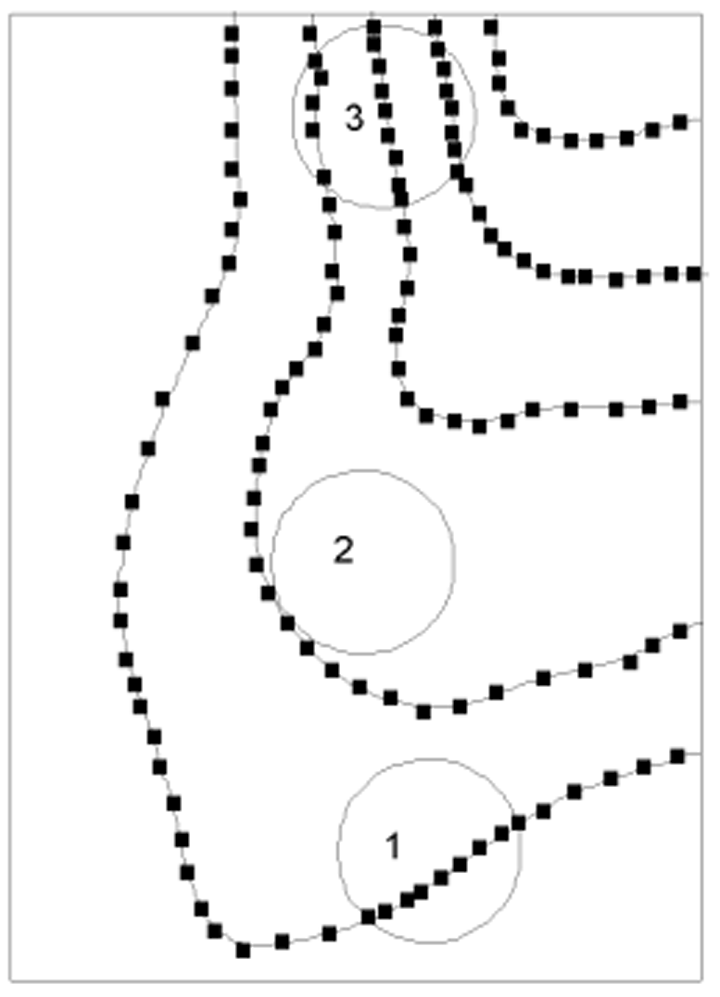
图9-10：等值线插值造成“阶梯地形”的原因

最好的解决方法是使用针对等高线插值的专用方法。如果没有合适的方法，最好把等高线数据点减少到最少，增加标识山峰、山脊、谷底和坡度突变的数据点，同时使用一个较大的搜索窗口。

3．4利用格网DEM提取等高线

在利用格网DEM生成等高线时，需要将其中的每个点视为一个几何点，而不是一个矩形区域，这样可以根据格网DEM中相邻四个点组成四边形进行等高线跟踪。其方法类似于后面描述的利用TIN提取等高线。实际上，也可以将每个矩形分割成为两个三角形，并应用TIN提取等高线算法，但是由于矩形有两种划分三角形的方法，在某些情况下，会生成不同的等高线（图9-11），这时需要根据周围的情况进行判断并决定取舍。

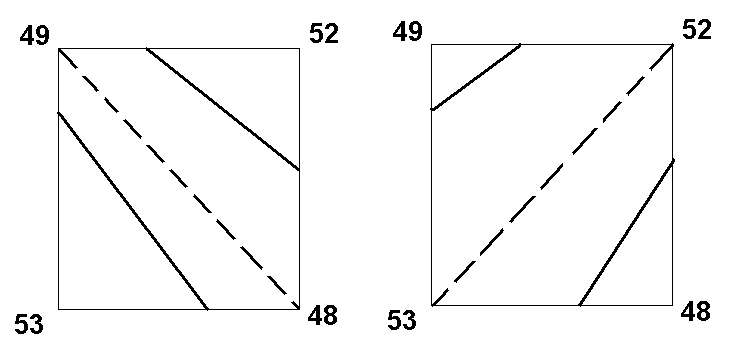
（a）                            (b)

图9-11：由于三角形划分不同造成生成等高线的不同

在格网DEM提取等高线中，除了划分为三角形之外，也可以直接使用四边形跟踪等高线。但是在图9-11所示的情形中，仍会出现等高线跟踪的二义性，即对于每个四边形，有两条等高线的离去边。进行取舍判断的方法一般是计算距离，距离近的连线方式优于距离远的连线方式。在图9-11种，就要采用（b）图所示的跟踪方式。

格网DEM提取等高线另一个值得注意的问题是，如果一些网格点的数值恰好等于要提取的等高线的数值，会使判断过程变得复杂，并且会生成不闭合的等高线，一般的解决办法是将这些网格点的数值增加一个小的偏移量。

3．5 TIN转成格网DEM

TIN转成格网DEM可以看作普通的不规则点生成格网DEM的过程。方法是按要求的分辨率大小和方向生成规则格网，对每一个格网搜索最近的TIN数据点，按线性或非线性插值函数计算格网点高程^*。