2．DEM的主要表示模型

2．1规则格网模型

规则网格，通常是正方形，也可以是矩形、三角形等规则网格。规则网格将区域空间切分为规则的格网单元，每个格网单元对应一个数值。数学上可以表示为一个矩阵，在计算机实现中则是一个二维数组。每个格网单元或数组的一个元素，对应一个高程值，如图9-2所示。

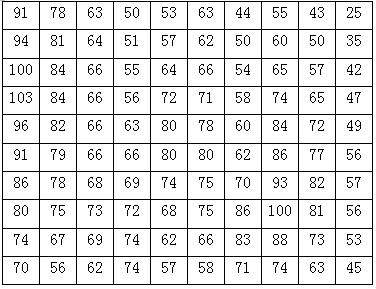
图9-2：格网DEM

对于每个格网的数值有两种不同的解释。第一种是格网栅格观点，认为该格网单元的数值是其中所有点的高程值，即格网单元对应的地面面积内高程是均一的高度，这种数字高程模型是一个不连续的函数。第二种是点栅格观点，认为该网格单元的数值是网格中心点的高程或该网格单元的平均高程值，这样就需要用一种插值方法来计算每个点的高程。计算任何不是网格中心的数据点的高程值，使用周围4个中心点的高程值，采用距离加权平均方法进行计算，当然也可使用样条函数和克里金插值方法。

规则格网的高程矩阵，可以很容易地用计算机进行处理，特别是栅格数据结构的地理信息系统。它还可以很容易地计算等高线、坡度坡向、山坡阴影和自动提取流域地形，使得它成为DEM最广泛使用的格式，目前许多国家提供的DEM数据都是以规则格网的数据矩阵形式提供的。格网DEM的缺点是不能准确表示地形的结构和细部，为避免这些问题，可采用附加地形特征数据，如地形特征点、山脊线、谷底线、断裂线，以描述地形结构。

格网DEM的另一个缺点是数据量过大，给数据管理带来了不方便，通常要进行压缩存储。DEM数据的无损压缩可以采用普通的栅格数据压缩方式，如游程编码、块码等，但是由于DEM 数据反映了地形的连续起伏变化，通常比较“破碎”，普通压缩方式难以达到很好的效果；因此对于网格DEM数据，可以采用哈夫曼编码进行无损压缩；有时，在牺牲细节信息的前提下，可以对网格DEM进行有损压缩，通常的有损压缩大都是基于离散余弦变换（Discrete Cosine Transformation，DCT）或小波变换（Wavelet Transformation）的，由于小波变换具有较好的保持细节的特性，近年来将小波变换应用于DEM数据处理的研究较多。

2．2等高线模型

等高线模型表示高程，高程值的集合是已知的，每一条等高线对应一个已知的高程值，这样一系列等高线集合和它们的高程值一起就构成了一种地面高程模型。如图9-3所示。

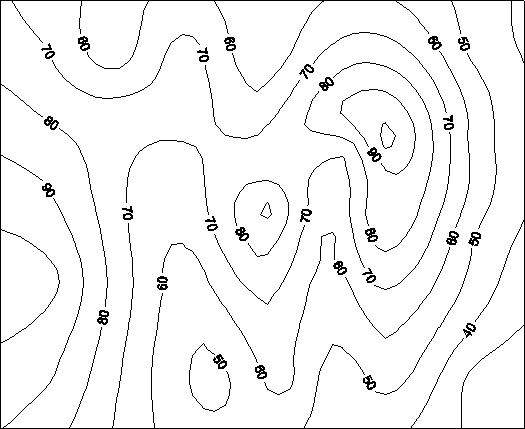
图9-3：等高线

等高线通常被存成一个有序的坐标点对序列，可以认为是一条带有高程值属性的简单多边形或多边形弧段。由于等高线模型只表达了区域的部分高程值，往往需要一种插值方法来计算落在等高线外的其它点的高程，又因为这些点是落在两条等高线包围的区域内，所以，通常只使用外包的两条等高线的高程进行插值。

等高线通常可以用二维的链表来存储。另外的一种方法是用图来表示等高线的拓扑关系，将等高线之间的区域表示成图的节点，用边表示等高线本身。此方法满足等高线闭合或与边界闭合、等高线互不相交两条拓扑约束。这类图可以改造成一种无圈的自由树。下图为一个等高线图和它相应的自由树（图9-4）。其它还有多种基于图论的表示方法。

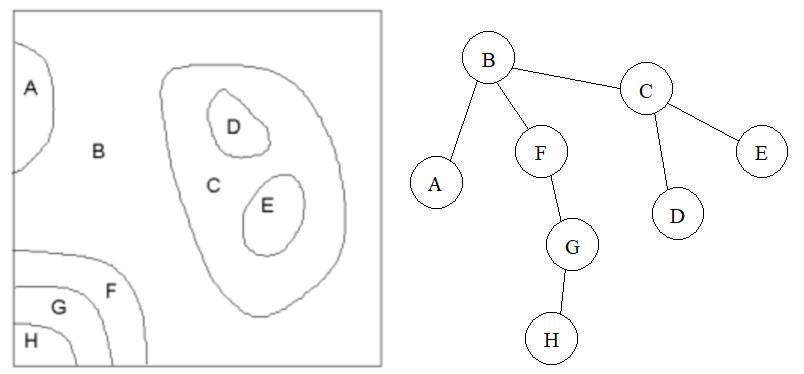
图9-4：等高线和相应的自由树

2．3不规则三角网（TIN）模型

尽管规则格网DEM在计算和应用方面有许多优点，但也存在许多难以克服的缺陷：

1）在地形平坦的地方，存在大量的数据冗余；

2）在不改变格网大小的情况下，难以表达复杂地形的突变现象；

3）在某些计算，如通视问题，过分强调网格的轴方向。

不规则三角网（Triangulated Irregular Network, TIN）是另外一种表示数字高程模型的方法[Peuker等，1978]，它既减少规则格网方法带来的数据冗余，同时在计算（如坡度）效率方面又优于纯粹基于等高线的方法。

TIN模型根据区域有限个点集将区域划分为相连的三角面网络，区域中任意点落在三角面的顶点、边上或三角形内。如果点不在顶点上，该点的高程值通常通过线性插值的方法得到（在边上用边的两个顶点的高程，在三角形内则用三个顶点的高程）。所以TIN是一个三维空间的分段线性模型，在整个区域内连续但不可微。

TIN的数据存储方式比格网DEM复杂，它不仅要存储每个点的高程，还要存储其平面坐标、节点连接的拓扑关系，三角形及邻接三角形等关系。TIN模型在概念上类似于多边形网络的矢量拓扑结构，只是TIN模型不需要定义“岛”和“洞”的拓扑关系。

有许多种表达TIN拓扑结构的存储方式，一个简单的记录方式是：对于每一个三角形、边和节点都对应一个记录，三角形的记录包括三个指向它三个边的记录的指针；边的记录有四个指针字段，包括两个指向相邻三角形记录的指针和它的两个顶点的记录的指针；也可以直接对每个三角形记录其顶点和相邻三角形（图9-5）。每个节点包括三个坐标值的字段，分别存储X，X，Z坐标。这种拓扑网络结构的特点是对于给定一个三角形查询其三个顶点高程和相邻三角形所用的时间是定长的，在沿直线计算地形剖面线时具有较高的效率。当然可以在此结构的基础上增加其它变化，以提高某些特殊运算的效率，例如在顶点的记录里增加指向其关联的边的指针。

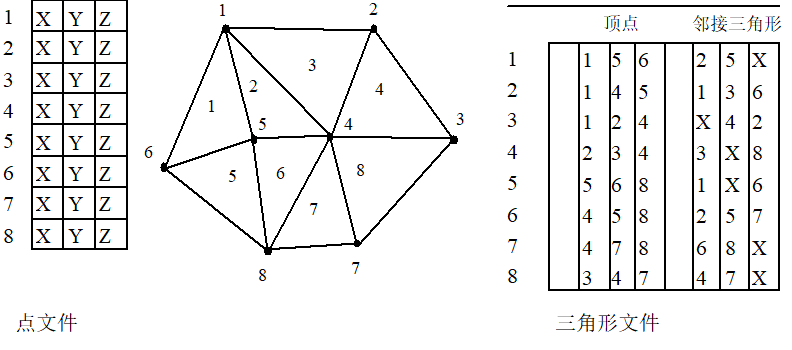
图9-5：三角网的一种存储方式

不规则三角网数字高程由连续的三角面组成，三角面的形状和大小取决于不规则分布的测点，或节点的位置和密度。不规则三角网与高程矩阵方法不同之处是随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置，因而它能够避免地形平坦时的数据冗余，又能按地形特征点如山脊、山谷线、地形变化线等表示数字高程特征。

2．4层次模型

层次地形模型（Layer of Details，LOD）是一种表达多种不同精度水平的数字高程模型。大多数层次模型是基于不规则三角网模型的，通常不规则三角网的数据点越多精度越高，数据点越少精度越低，但数据点多则要求更多的计算资源。所以如果在精度满足要求的情况下，最好使用尽可能少的数据点。层次地形模型允许根据不同的任务要求选择不同精度的地形模型。层次模型的思想很理想，但在实际运用中必须注意几个重要的问题：

1）层次模型的存储问题，很显然，与直接存储不同，层次的数据必然导致数据冗余。

2）自动搜索的效率问题，例如搜索一个点可能先在最粗的层次上搜索，再在更细的层次上搜索，直到找到该点。

3）三角网形状的优化问题，例如可以使用Delaunay三角剖分。

4）模型可能允许根据地形的复杂程度采用不同详细层次的混合模型，例如，对于飞行模拟，近处时必须显示比远处更为详细的地形特征。

5）在表达地貌特征方面应该一致，例如，如果在某个层次的地形模型上有一个明显的山峰，在更细层次的地形模型上也应该有这个山峰。

这些问题目前还没有一个公认的最好的解决方案，仍需进一步深入研究。