1. 正交实验设计法测试原理
正交实验设计法(Orthogonal Experimental Design)是指从大量的实验点中挑选出适量的、有代表性的点，应用Glois理论导出的“正交表”，合理地安排实验的一种实验设计方法。正交实验设计法是研究多因素多水平的一种实验方法，一般用在输入条件相互独立，并且需要对输入条件的各种组合进行测试的场合。
正交实验设计法包含2个关键因素，具体如下所示。
(1)因子: 因子也称为因素，是指所有影响实验指标的条件。
(2)因子的状态: 因子的状态也叫因子的水平，它指的是因子变量的取值。
软件功能测试的目的是检查被测软件是否满足其规格说明书中规定的功能需求，利用正交实验设计法来设计测试用例时，首先要根据被测软件的规格说明书找出影响其功能实现的操作对象和外部因素，把他们称为因子，而把各个因子的取值当做状态，构造出二元的因素分析表。然后利用正交表进行个因子的状态的组合，构造有效的测试输入数据集，并由此建立因果图。这样得出的测试用例集，测试用例的数目将大大减少。
2. 正交实验法设计测试用例步骤
利用正交实验设计法设计测试用例时，可以按照如下步骤进行。
（1）提取因子，构造因子状态表。
分析软件的规格需求说明得到影响软件功能的因子，确定因子可以有哪些取值，即确定因子的状态。例如，某一软件的运行受到操作系统和数据库的影响，因此影响其运行是否成功的因子有操作系统和数据库２个，而操作系统有Windows、Linux、Mac3个取值，数据库有Mysql、SqlServer、Oralce3个取值，因此操作系统的因子状态为３，数据库因子状态为3，据此构造的因子-状态表如下表所示。
表2-4-1 因子-状态表
因子 | ||
操作系统 | 数据库 | |
因子的状态 | windows | mysql |
linux | SqlServer | |
mac | Oralce | |
（2）加权筛选，简化因子－状态表。在实际软件测试中，软件的因子及因子的状态会有很多，每个因子及其状态对软件的作用也大不相同，如果把这些因子及状态都划分到因子－状态表中，最后生成的测试用例会相当庞大，从而影响软件测试的效率，因此需要根据因子及状态的重要程度进行加权筛选，选出重要的因子与状态，简化因子－状态表。
（3）利用正交表构造测试数据集。
正交表的表示形式为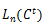
。
v Ｌ表示正交表。
v ｎ为正交表的行数，正交表的每一行可以设计一个测试用例，因此行数ｎ也表示可以设计的测试用例的数目。
v C表示正交实验的因子数目，即正交表的列数，因此正交表是一个ｎ行ｃ列的表。
v t称为水平数，表示每个因子能够取得的最大值，即因子有多少个状态。
例如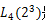
是最简单的正交表，它表示该实验有3个因子，每个因子有两个状态，可以做４次实验，如果用0和1表示每个因子的两种状态，则该正交表就是一个，4行3列的表，如下表所示。
表2-4-2 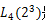正交表
序号 | 1 | 2 | 3 |
1 | 0 | 0 | 0 |
2 | 0 | 1 | 1 |
3 | 1 | 0 | 1 |
4 | 1 | 1 | 0 |
假设表2-4-2中的3个因子为登录用户名、密码和验证码，用户名、密码和验证码有正确(用1表示)和错误(用0表示)两种状态，正常需要设计23＝8个测试用例，而使用正交表只需要设计４个测试用例就可以达到同样的测试效果。因此，正交实验法是一种高效、快速、经济的实验设计方法。上述例子中3个因子的状态都是两种，这样的正交实验比较容易设计正交表，但在实际软件测试中，大多数情况下，软件有多个因子，每个因子的状态数目都不相同，即各列水平数不等，这样的正交表称为混合正交表，如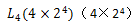
这个正交表表示有１个因子有４种状态，有2个因子有4种状态。
实例：在企业信息系统中，在员工信息查询页面，有3个独立的查询条件：员工号、员工姓名和员工邮件地址，每个条件可以填和不填，请使用正交表设计法设计测试用例。
（1）提取因子，构造因子状态表。
员工信息查询页面有3个因子：员工号、员工姓名和员工邮件地址，每个因子有2个2个状态，具体的因子-状态表如下表所示。
表2-4-3 因子-状态表
因子 | |||
员工号 | 员工姓名 | 员工邮件地址 | |
因子的状态 | 填 | 填 | 填 |
空 | 空 | 空 | |
（2）简化因子－状态表。由于员工信息查询页面的因子和因子状态都比较简单，不需要简化。
（3）利用正交表构造测试数据集。根据因子数是3、因子的状态（水平数）是2和行数取最小值，选择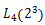
正交表，根据正交表的内容得到所需的测试用例，具体如下所示。
因子数 | ||||
水平数 | 1 | 2 | 3 | |
1 | 0 | 0 |
| |
2 | 0 | 1 | 1 | |
3 | 1 | 0 | 1 | |
4 | 1 | 1 | 0 | |
因子数 | ||||
水平数 | 1 | 2 | 3 | |
1 | 填 | 填 | 填 | |
2 | 填 | 空 | 空 | |
3 | 空 | 填 | 空 | |
4 | 空 | 空 | 填 | |
图2-4-1 正交表构建并转化为测试用例
3. 正交实验设计法优点
利用正交实验设计法设计测试用例，比使用等价类划分、边界值分析、决策表等方法具有如下优点：
（1）节省测试工作工时。由于把实验设计法的正交表直接应用到因素分析表。简单地设定测试用例，比其他设计测试用例的方法要单纯，不一定非要具备丰富的经验与创造力，可以减轻测试者的负担。
（2）可控制生成的测试用例的数量。若考虑各因子的所有状态的组合来设计测武用例，从测试工作量和所用时间等方面来看，是不可能实现的。利用加权筛选，考虑各因子与状态的重要程度及因子间的相互影响，做出一定的筛选，可以把生成的测试用例的数量控制在允许的范围内。
（3）测试用例具有一定的覆盖度。实验设计法是一种合理的、有效的抽样方法，对被测软件来说，测试用例的涉及范围在整体上比较均匀，可排除偏向于功能的某个局部的可能性，与结构测试相配合，可检出软件中大部分错误，检出故障率达50%以上。
