在数字电路理论中,时序逻辑电路是指电路任何时刻的稳态输出不仅取决于当前的输入,还与前一时刻输入形成的状态有关。这跟组合逻辑电路相反,组合逻辑的输出只会跟目前的输入成一种函数关系。换句话说,时序逻辑拥有储存元件(内存)来存储信息,而组合逻辑则没有。
从时序逻辑电路中,可以建出两种形式的有限状态机:
摩尔型有限状态机:输出只跟内部的状态有关。(因为内部的状态只会在时脉触发边缘的时候改变,输出的值只会在时脉边缘有改变)
米利型有限状态机:输出不只跟目前内部状态有关,也跟现在的输入有关系。
时序逻辑因此被用来建构某些形式的电脑的内存,延迟跟储存单元,以及有限状态自动机。大部分现实的电脑电路都是混用组合逻辑跟时序逻辑。
时序逻辑电路特点:
功能特点:电路在某采样周期内的稳态输出Y(n),不仅取决于该采样周期内的“即刻输入X(n)”,而且还与电路原来的状态Q(n)有关。(通常Q(n)记录了以前若干周期内的输入情况)
结构特点:除含有组合电路外,时序电路必须含有存储信息的有记忆能力的电路:触发器、寄存器、计数器等。
时序逻辑电路框图:
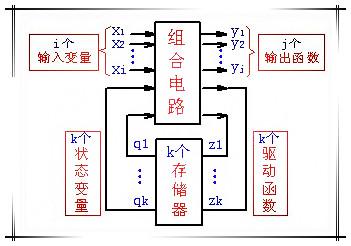
时序逻辑电路分类:
一、按“功能、用途”分为:
1.寄存器;
2.计数(分频)器;
3.顺序(序列)脉冲发生器;
4.顺序脉冲检测器;
5.码组变换器;…
二、按各触发器的“动作特性” 分为:
1.同步时序电路:电路中所有触发器的状态变化同步进行。其时钟方程:CP1= CP2=…= CPK= CP↓(或CP↑)。即:所有CP端联在一起,由CP信号同一有效沿触发。
2.异步时序电路:
3.电路中根本没有CP同步信号。
4.各触发器不是用同一CP脉冲的同一有效沿触发的。
三、摩尔(Moore)型和米里(Mealy)型
1.摩尔型:电路的输出Yn,只取决于各触发器的输出Q n,而与外输入X n无关。即:Yn=F(Q n)。
2.米里型:电路的输出Yn,不仅取决于各触发器的输出Q n,而且还与外输入X n有关。即:Yn=F(Q n,X n)。
四、“完全描述的”和“非完全描述的”含有K个状态变量(K个触发器)的时序电路,最多可描述K个不同状态。
1.若电路功能必须用 个状态来描述,则称之为“完全描述的”(二进制的);
2.若只用 个状态中的一部分来描述,则称之为“非完全描述的”(非二进制的)。


