一个逻辑函数的表达式可以是多种多样的，通过布尔代数的公式可以将函数的表达式从一种形式转换为另一种形式。例如：

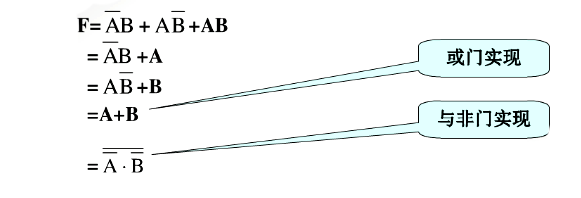
标准形式

逻辑函数有“最小项之和”及“最大项之积”两种标准形式。

表示方法

◆布尔代数法

按一定逻辑规律进行运算的代数。与普通代数不同，布尔代数中的变量是二元值的逻辑变量。

◆真值表法

采用一种表格来表示逻辑函数的运算关系，其中输入部分列出输入逻辑变量的所有可能组合，输出部分给出相应的输出逻辑变量值。

◆逻辑图法

采用规定的图形符号，来构成逻辑函数运算关系的网络图形。

◆卡诺图法

卡诺图是一种几何图形，可以用来表示和简化逻辑函数表达式。

◆波形图法

一种表示输入输出变量动态变化的图形，反映了函数值随时间变化的规律。

◆点阵图法

是早期可编程逻辑器件中直观描述逻辑函数的一种方法。

◆ 硬件设计语言法

是采用计算机高级语言来描述逻辑函数并进行逻辑设计的一种方法，它应用于可编程逻辑器件中。目前采用最广泛的硬件设计语言有ABLE-HDL、VHDL等。