浮点数

浮点数是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。具体的说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学计数法。

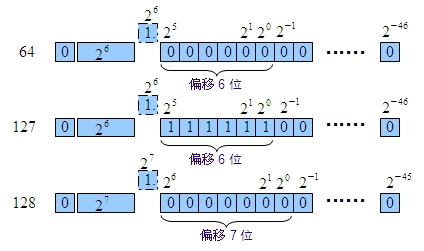
标准保存

以下内容需要知道二进制小数转换十进制计算方法和整数一样，都是对每一位用2的幂加权。

IEEE浮点标准用 V = (-1）^s * M * 2^E的形式表示

V就是值

符号（sign)s决定正负，对于0有特殊处理

有效数（significand)M是一个二进制小数，范围在1~2或0~1之间

指数（exponent)E是2的幂（可以是负数），对浮点数加权

浮点数划分成3个域

一个单独符号位编码s

k位指数域 exp = e(k-1）...e⑴e(0）编码指数E

n位小数域 frac = f(n-1）...f⑴f(0）编码有效数M，但被编码的值依赖于指数域是否为零。

在C/C++中的float下 s有1位，exp有k=8位，frac有n=23位，double变量下k=11,n=52

根据exp的值，编码分三种状况：

规格化值

最普遍的状况，当exp的位模式既不是全为0也不是全为1时，就都属于这种状况。此时，指数域解释为偏置形式，E = e-Bias（e减Bias），e是无符号数，而Bias是一个等于2^(k-1） -1的偏置值。由此产生了指数的取值范围，float: -126~127，double: -1022~1023

小数域解释为描述小数值f，在0~1之间，有效数定义为M = 1+f，这样隐含了开头的1，免费获得了一个额外的精度位

非规格值

指数域全为0，就是非规格化的值，此时，指数值是 E = 1 - Bias(Bias定义同上），有效数的值是 M = f，没有开头的1。值得注意的是这种方法对0的表示。+0.0的浮点表示中，位模式全为0：符号位是0，指数域全0，小数域也是0。而-0.0只有符号位是1，其他全0

特殊值

指数域全为1，就是这类数。

当小数域全为0时，得到的值表示无穷，s=0正无穷，s=1负无穷。当这两个非常大的数相乘或对某数除以0可以得到溢出的结果。当小数域非0时结果被称作NaN，即not a number。一些运算结果不能表示为无穷或实数，就返回NaN，例如对-1开根号。