一、“情境 +问题串”为有效教学提供主要脉络

十多年来，“问题情境——建立模型——解释与应用”的基本叙述方式己经成为这套教材的一个标志性特点，第4版在继承这个特色的基础上，形成了 “情境+问题串”的呈现形式，成为独到的特色。

也就是每一个单元每一个重要内容的呈现都力图从学生喜闻乐见的一个或一组与课程内容有内在联系的特定情境出发，设计一组问题，学生在教师引导下理解情境、解决问题的过程就是学习数学、发展数学、实现数学课程目标的过程。这样，使课程内容的展开过程与学生的学习过程、教师的教学过程和课程目标的达成过程实现统一。

这样一种稳定的、具有较强包容性的呈现形式，无疑有助于为广大一线教师准确理解和把握教材特点以及教与学的要求，促进教师创造性开展数学教学活动。

二、有机整合多维度的学习目标

这套教材特别重视学生在知识技能、数学思考、解决问题和情感态度等各方面的全面发展，促进在教学过程中学习目标的整体实现。

（一）注重基本思想和基本活动经验

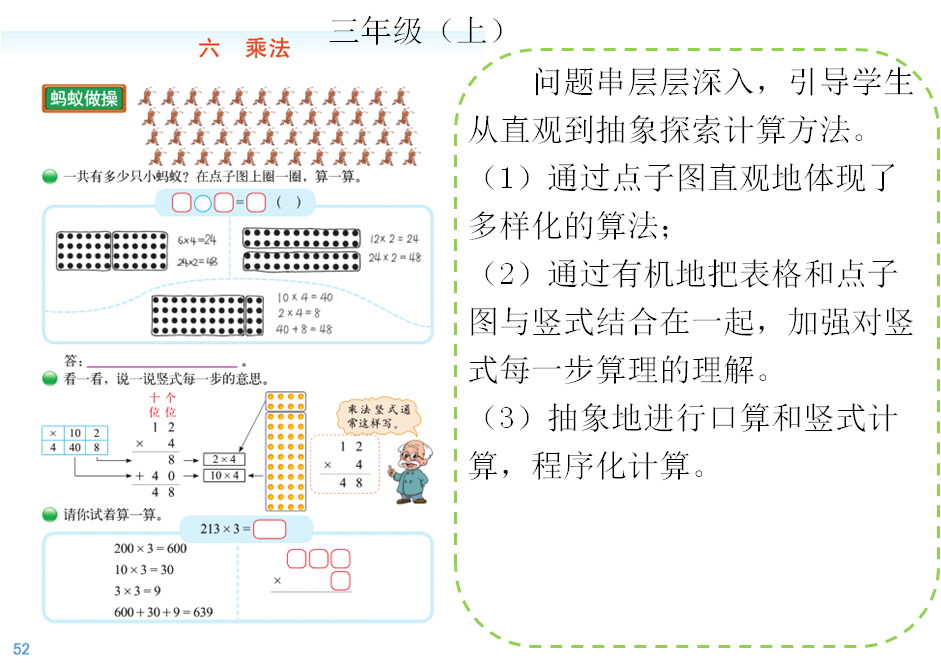
对于数学的基本思想，教材力求通过设计活动和问题，处处体现抽象、推理和模型思想。例如对于“数的认识”，非常重视从数量到数的抽象过程，在一上第4页“快乐的家园”，体现出从 1个太阳、1棵树、1个萝卜、1筐萝卜等数量中抽象出数“1”的过程，以及从其他数量中抽象出其他数的过程。

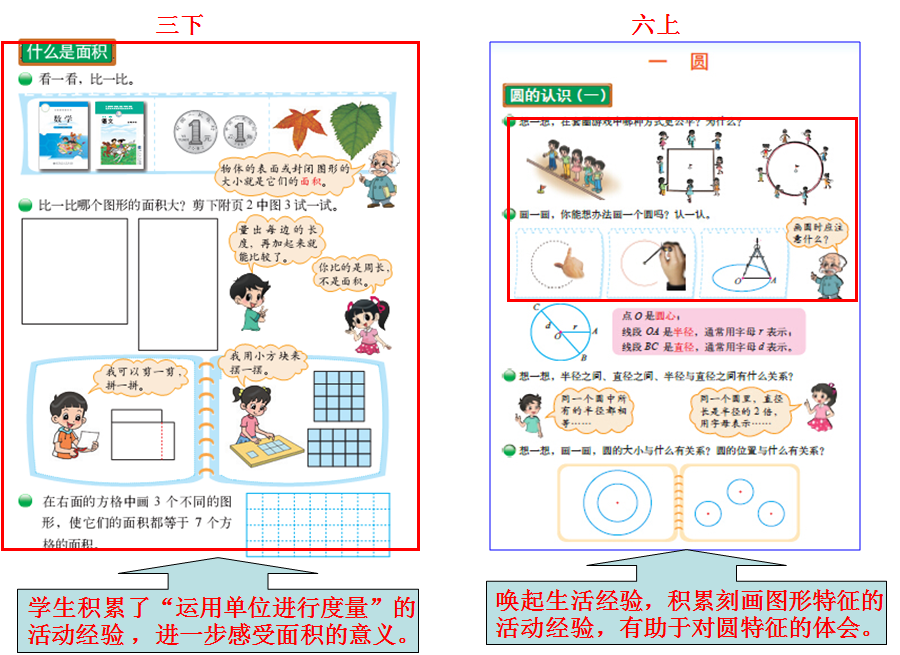
第一，设计专门的积累活动经验的课，在这些课中一般不以学习某个具体的概念为目标，而是通过设计活动帮助学生积累从事数学活动的经验和数学思考的经验。 

第二，在一节课学习的“问题串”中，设计积累活动经验的活动和问题。

（一）注重基本思想和基本活动经验

基本数学思想方面：

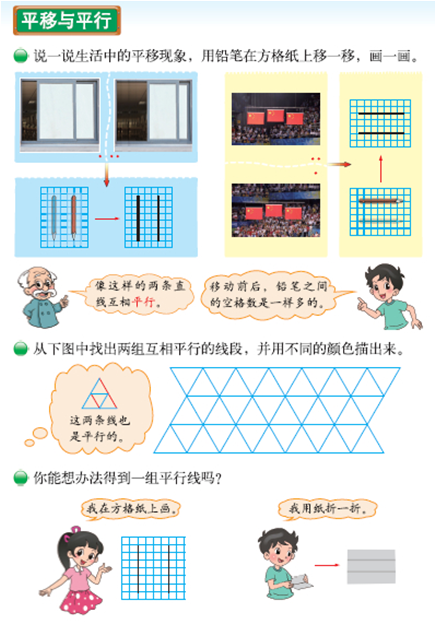
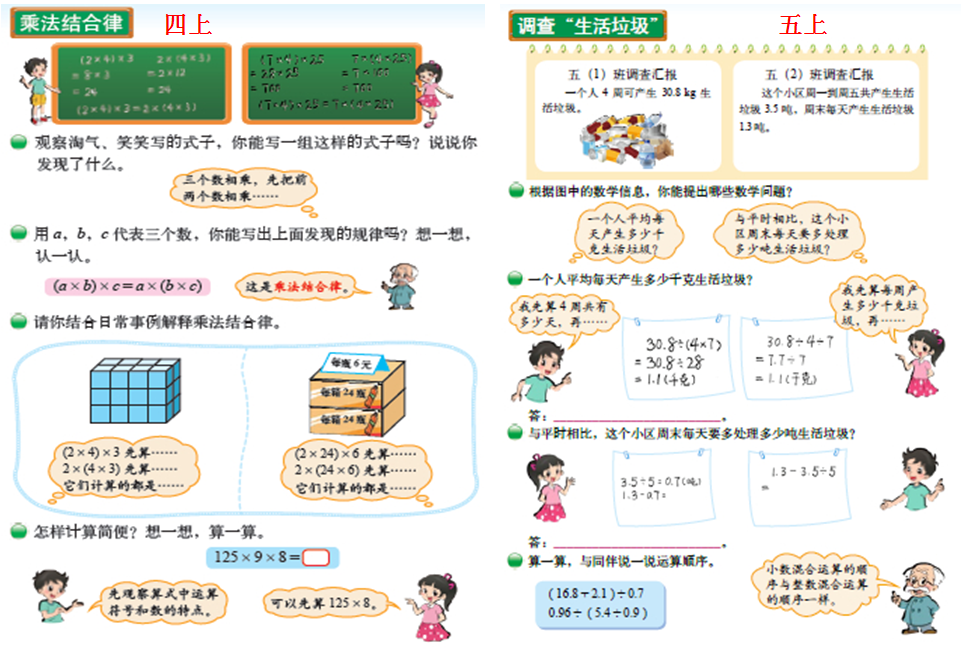
抽象思想：体现从数量到数、从物体到图形的抽象，以及从数到字母的抽象。

推理思想：既体现归纳、类比等合情推理，鼓励学生进行猜想；又针对小学生的特点，鼓励学生运用自己的语言和多种方式说明道理。

模型思想：体现数学建模的全过程。

到处体现基本的数学思想。

（二）注重 “从头到尾”思考问题的过程

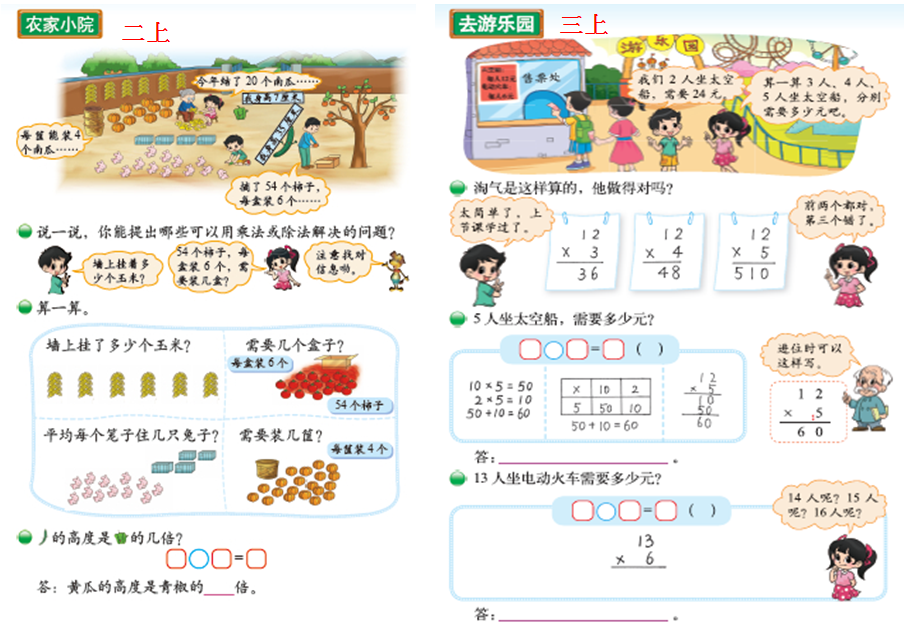
首先是在基础知识与基本技能的学习中，鼓励学生发现和提出问题，然后鼓励学生分析和解决问题，如一下的“采松果”；

教材还设计了专门培养学生发现和提出问题能力的活动，如在整理与复习中，专门设立了“我提出的问题”的栏目，鼓励学生在回顾整理的基础上再提出新的问题；

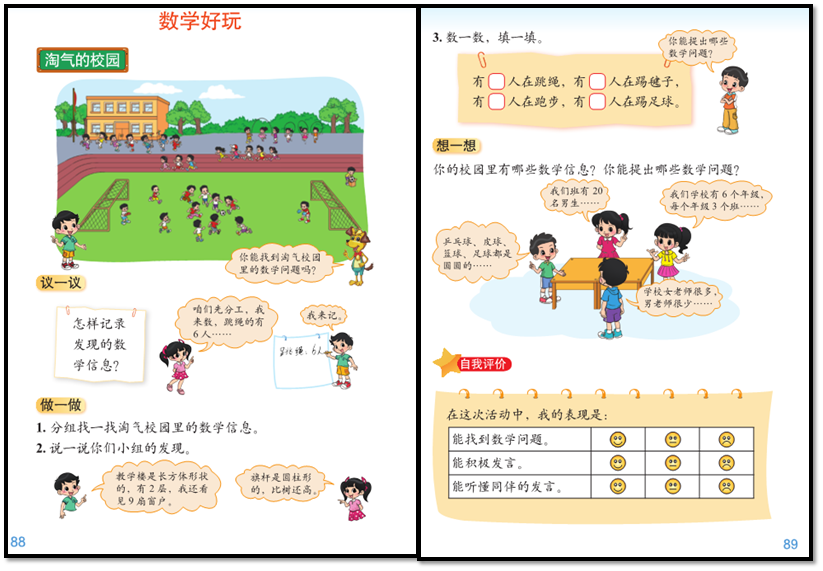
还有，“综合与实践活动”内容的设计，第一学段通过“议一议”、“做一做”、“想一想”，第二学段通过“设计活动方案”、“实际活动”、“总结反思”等活动过程，鼓励学生 “从头到尾”地思考问题；

同时，每学期都安排了“问题银行”，鼓励学生将自己提出的当时没有解决的问题存入“问题银行”。 

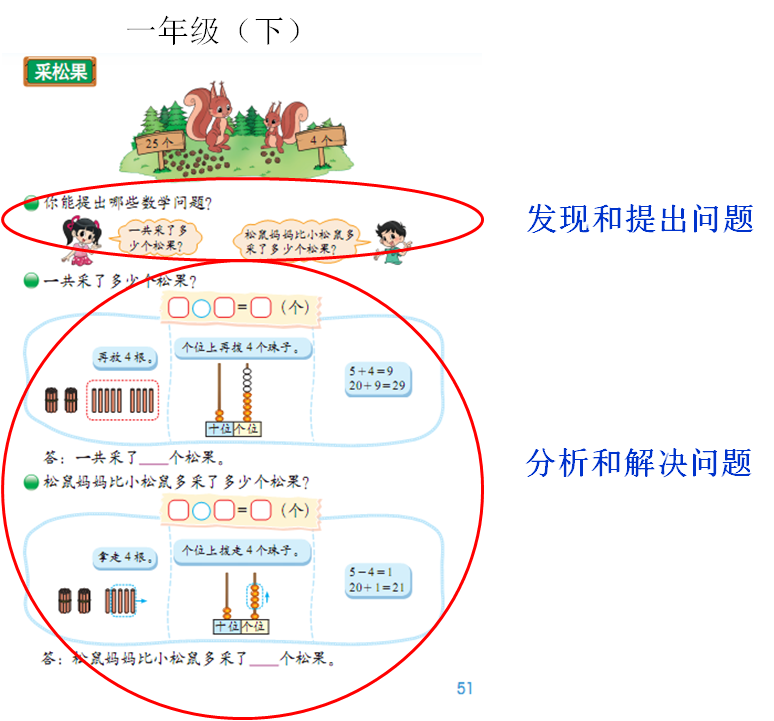
首先鼓励学生发现和提出问题；然后鼓励学生分析和解决问题。 

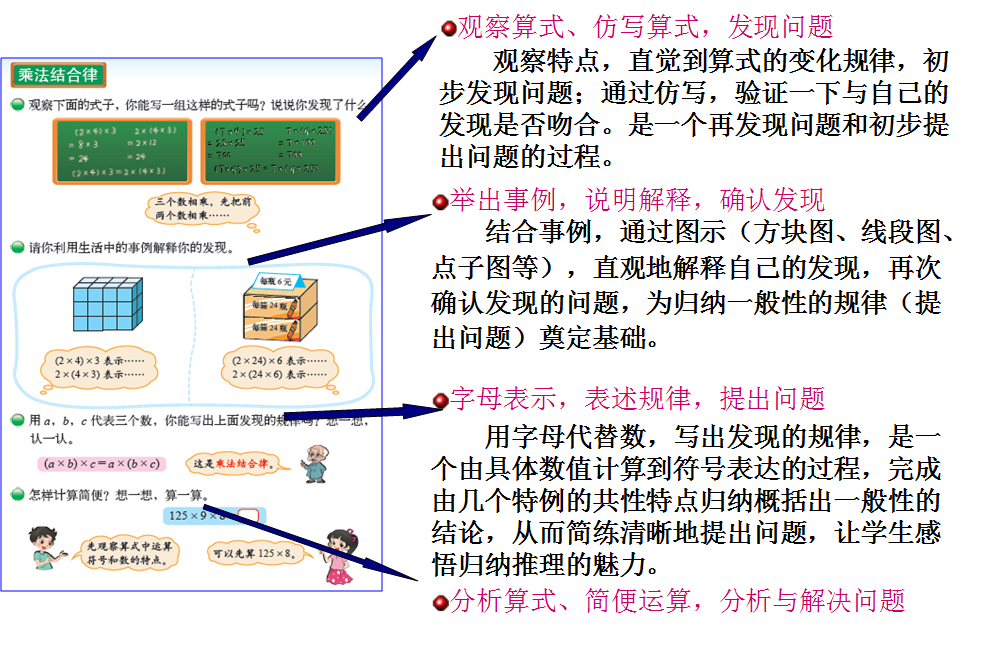
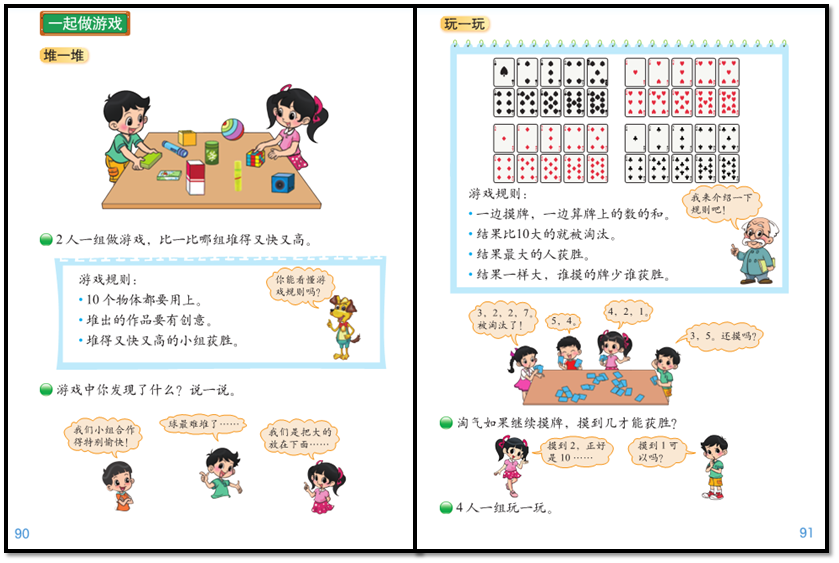
综合与实践第一阶段：

学生发现和提出问题是基于表面信息直接提出的。

学生可能提出球反弹的高度与什么因素有关？关系是什么？如何刻画等问题。

综合与实践第二阶段:鼓励学生提出更深层次的问题。

二、有机整合多维度的学习目标

（三）注重让学生学习理解的数学

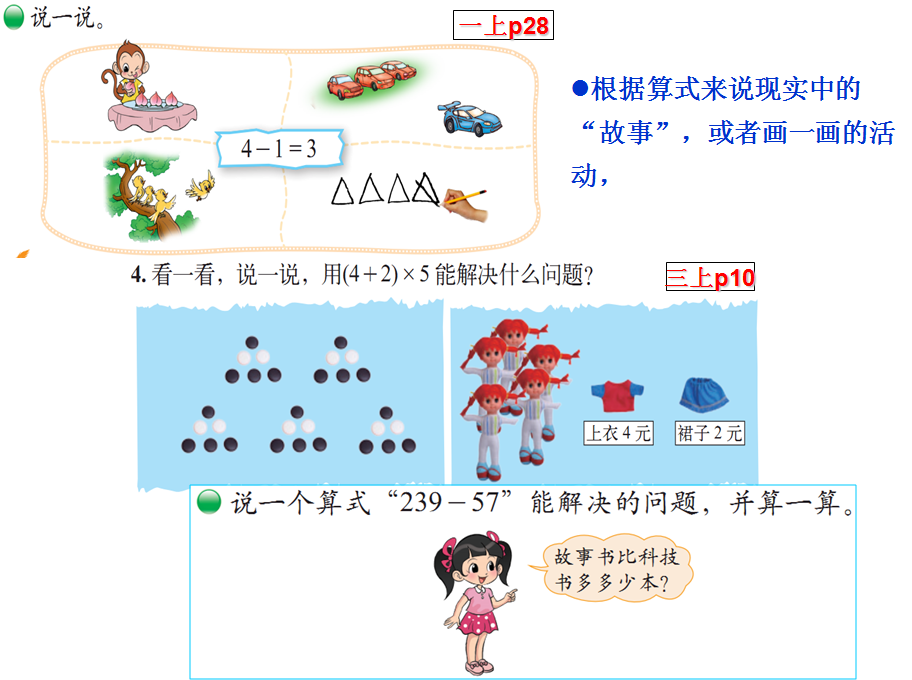
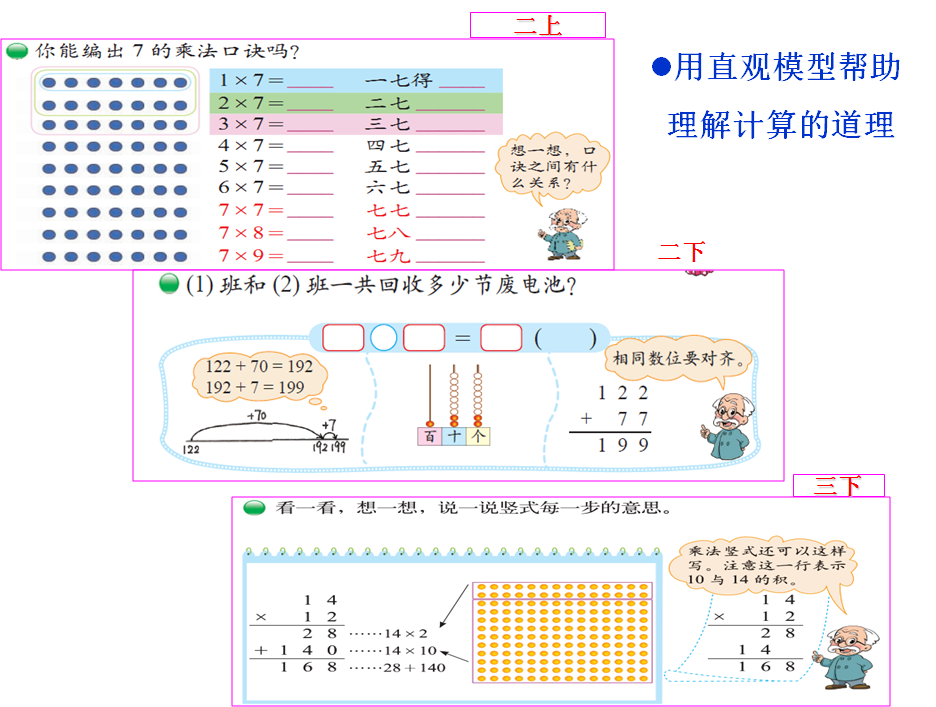
为了提高学生对于基础知识的理解和基本技能的形成，教材内容的呈现体现了知识的形成过程、多角度理解以及对知识与技能的应用。特别重视多角度理解，鼓励学生举例、解释、描述、联系，还通过提供学具操作、图形直观等形式为学生理解提供适当的“脚手架”。

例如，重视对运算意义的理解。

用从多个情境中抽象出运算过程；

（四）注重学习兴趣和习惯的培养

激发学生的学习兴趣:通过呈现丰富的情境、设计挑战性的问题、呈现方式的多样性、感受数学的价值等来体现。

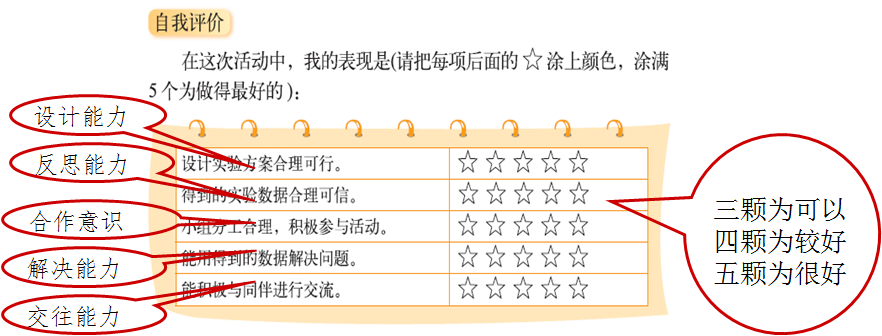
（2）培养学生的数学学习习惯：对于反思习惯，教材通过多种层次的活动鼓励学生对于学习过程和学习结果进行评估和总结。

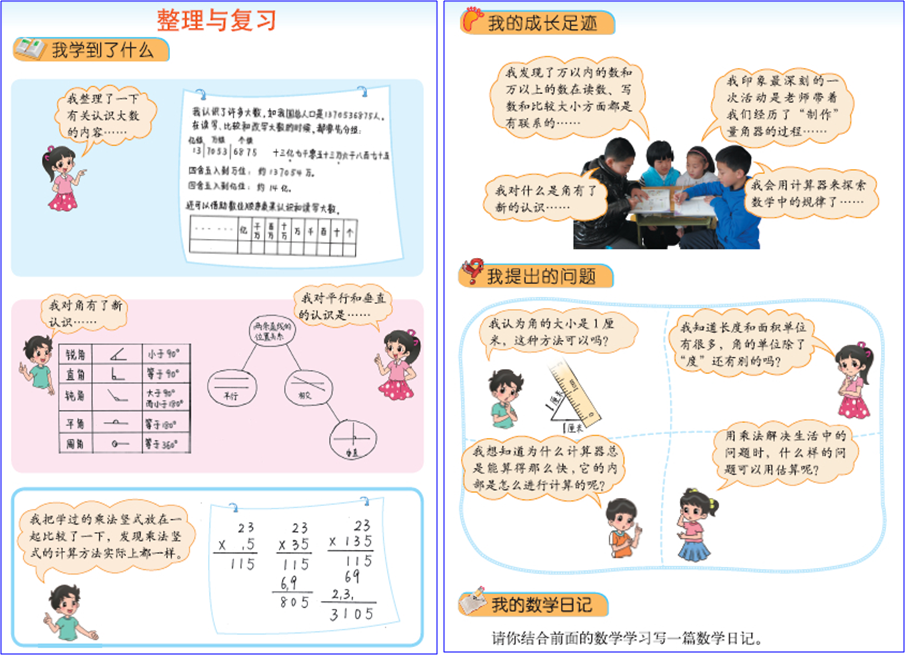
如在每学期都安排整理与复习、总复习，鼓励学生进行阶段总结。不仅仅是设计一些题目，更设计了“回顾整理”、“回顾与交流”帮助学生通过解决问题回顾学习过程、整理学习内容，同时体现学生的成长足迹。

在综合与实践中，安排了学生自评的活动。

三、丰富的题材激发对新知的探索

教材一直关注设计有趣的、现实的、蕴涵数学意义和富有挑战性的情境，这构成了教材的鲜明特点。同时，情境设计上也注重题材的多样与丰富，具有一定的通识性，是广大小朋友都喜欢和能感受到的，如童话、寓言、游戏、环保、体育等题材；同时教材还充分关注了农村题材，纯城市题材与纯农村题材基本均衡。     

第一学段的情境主要来源于儿童的日常生活和学校生活，让学生感到亲切，有生活经验，有助于对数学内容的理解。

第二学段增加了社会生活情境的比例和适当的来源于数学内部的情境，拓宽学生的视野，让学生感受到数学的博大。

另外，教材还结合具体的知识点，选择恰当的形成呈现相应的数学史，发掘数学发展史的教育价值，这样有机的结合，能让学生感受到数学的发生、发展过程，改变过去用数学史“点缀”教学内容的两张皮现象，从而增进了教材的文化意蕴和数学内涵。

四、练习题的形式多样而又有层次性

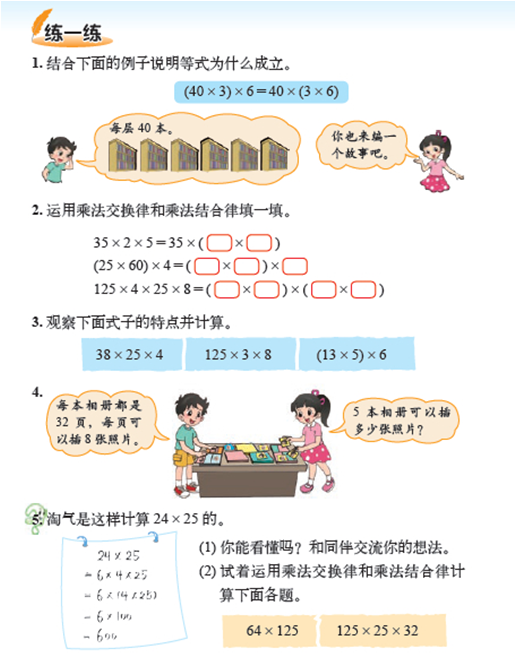
数量上，1 课时 2 页的内容，其中包括 1 页练一练；2 课时 3 页的内容，其中包括 1.5 页的练一练。正文和练习的页码比例达到 1︰1。

层次上，设计了基本练习、变式练习、拓展练习等层次，避免了 “跳跃性”较大的现象。一般是3:2:1。

维度上，注重形式多样，通过设计（事实性）知识和技能、数学理解、解决（常规）问题、联系拓展等维度，体现对于学习内容不同方面的要求。特别重视开发了一批数学理解的题目，促进学生对所学内容的理解。

五、为学生提供个性化的学习机会

“不同的学生在数学上获得不同的发展”这一现代数学教育理念，一直为各版本的教材所重视。此教材在尊重学生发展的差异性方面有着深入的探索，力争为学生提供更多的个性化学习机会。

一方面，教材设计了拓展性问题和作业，提供了丰富的阅读材料，体现教材的弹性和可选择性。

另一方面，在面对同一个情境、同一句话语、同一个问题、同一个方法，尽可能关注学生个性化的学习过程，引导学生学会尊重并欣赏他人对于同一内容的不同理解，学会尊重并欣赏他人生活经验、思维方式的独特性和多样性，学会独立思考并积极与他人分享自己对问题的独特理解。如，呈现学生的多种想法，在综合与实践活动中鼓励学生获得不同的体验等。

所有这些，都是在试图传达这套教材在尊重每一个个体、体现人文关怀、倡导教育民主、鼓励独立思考与自由表达、提倡合作与交流等价值观念上的探索。 

总之，教材力求从学生经验出发，体现“从头到尾”思考问题的过程；突显数学活动经验、强调数学理解的学与教共进的过程中，达到基础知识、基本技能、基本思想、基本活动经验并重，发现和提出问题能力、分析和解决问题能力共同发展。