《课程标准》的要求

第一学段

○探索并掌握长方形、正方形的面积公式，会估计给定简单图形的面积（参见例13）。

第二学段

○探索并掌握三角形、平行四边形和梯形的面积公式，并能解决简单的实际问题。

○会用方格纸估计不规则图形的面积（参见例33）。

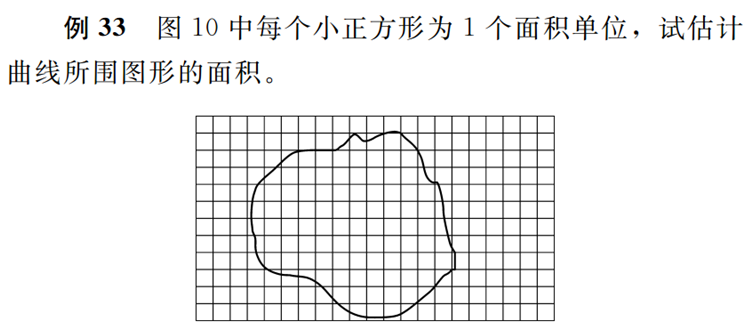
 ○例33说明

平行四边形面积教材分析

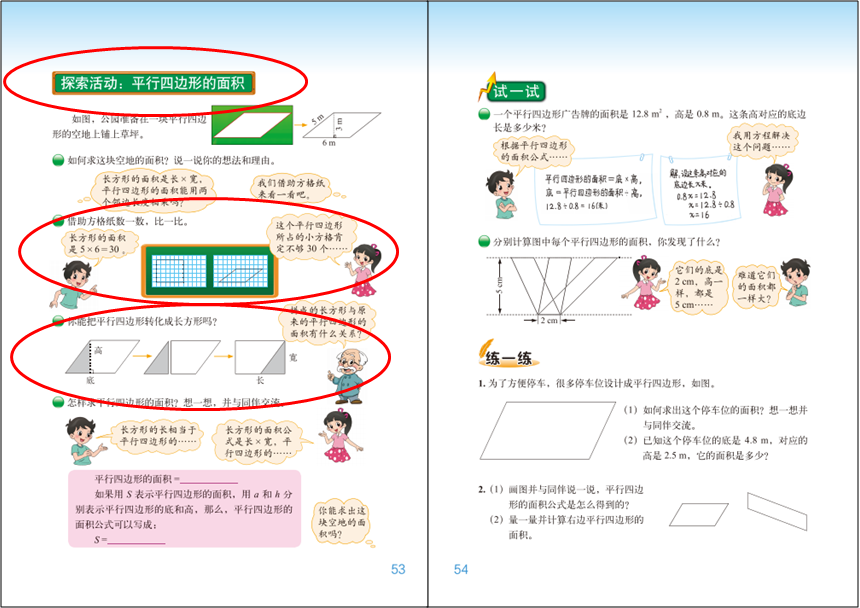
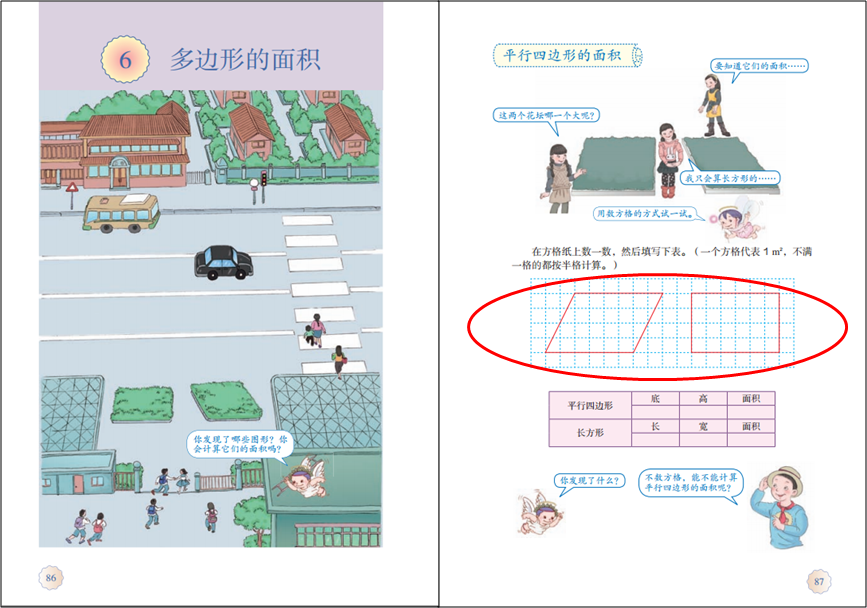
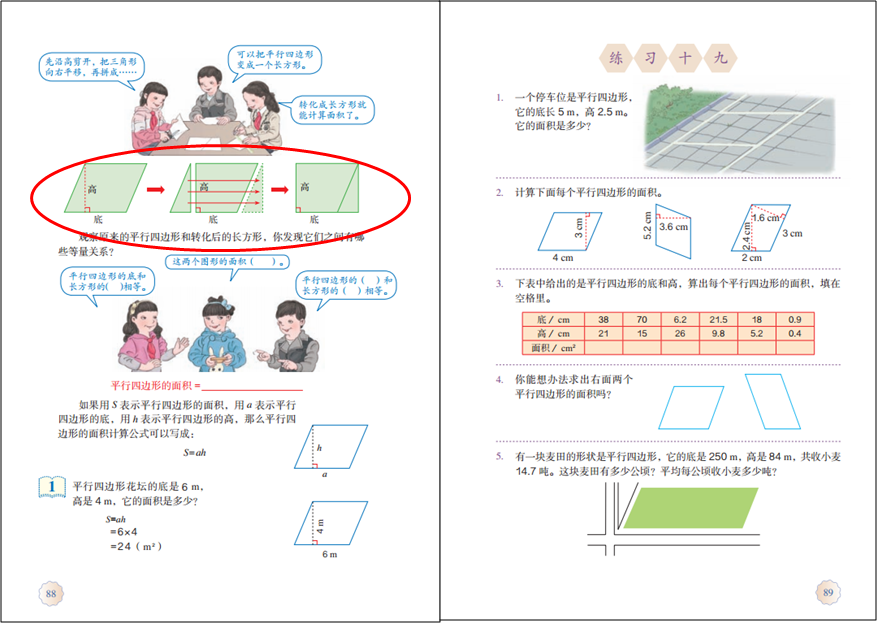
1.新知准备

2.导入情境

3.格子图的使用

4.公式推导

1.进一步强化对“面积”及“面积单位”的理解 

学生第一次学习面积是在长方形、正方形面积计算之前，建立了对面积概念的理解，规定了面积单位，这个理解在长方形、正方形面积计算公式的学习过程中又进一步加深，但并不是到此结束了。

学生学习平行四边形的面积时，教师应设计一些活动，如在格子图中数面积、辨析下面图形的面积是否发生变化等，让学生进一步明确面积及面积单位的含义 。 

2.正确把握《课标》对面积学习的要求 

《课标》在修订过程中，削弱了单纯的平面图形面积、体积、周长等计算，融计算公式的理解和掌握于探索和操作过程之中，强调要能够应用公式解决实际问题。因此教学中不能将主要精力放在套用公式进行计算上，以至于将这部分内容简单地处理成计算问题。 

3.设计操作活动，积累活动经验 

学生“四基”中的基本活动经验，不是靠被动的接受知识来积累的，而是靠学生亲历一些操作活动，在活动中积累的。教学中要设计实际的情境，让学生在探究活动中进行思考，经历观察、操作、归纳、概括、估计、猜想、验证、推理等学习的过程。 

4.重视直接测量 

教材编写是比较重视直接测量的，编写了“在格子图中数一数”等内容，这是让学生在数一数的过程中，进一步理解测量的本质、体会面积的含义等；另外还要通过直接测量来促进对间接测量方法的理解，及对面积体积计算公式的理解。 

5.重视数学思想方法 

规则图形周长、面积和体积测量公式探索的过程中，蕴含着丰富的数学思想方法，能够很好地落实让学生“感悟数学的基本思想”这一课程目标。就平行四边形而言，其面积计算的学习过程中，至少涉及化归思想、出入相补原理、推理能力等方面的培养。