暂无搜索结果
-
1 引言
-
1.1 高等数学简介
-
1.2 高等数学学习方法探究
-
2 第一章 函数、极限与连续
-
2.1 前言
-
2.2 函数
-
2.3 数列的极限
-
2.4 函数的极限
-
2.5 无穷小与无穷大
-
2.6 极限的运算
-
2.7 两个重要极限
-
2.8 等价无穷小的替换
-
2.9 函数的连续性
-
2.9.1 函数的间断点
-
2.9.2 初等函数的连续性
-
2.10 闭区间上连续函数的性质
-
2.11 数学实验 用MatLab绘图、求极限
-
2.12 第一章复习指导及章节测验
-
3 第二章 导数与微分
-
3.1 前言
-
3.2 导数的概念
-
3.2.1 导数的定义
-
3.2.2 可导与连续的关系
-
3.3 导数的运算
-
3.3.1 函数的四则运算求导法则
-
3.3.2 复合函数求导法则
-
3.3.3 隐函数求导
-
3.3.4 反函数求导
-
3.4 由参数方程所确定的函数的导数
-
3.5 高阶导数
-
3.6 微分
-
3.7 数学实验 用MatLab求导数
-
4 第三章 导数的应用
-
4.1 前言
-
4.2 中值定理
-
4.3 洛必达法则
-
4.4 函数的单调性、曲线的凹凸性与拐点
-
4.5 函数的极值与最值
-
4.6 边际与弹性
-
4.7 用MatLab求一元函数的最大值与最小值
-
5 不定积分
-
5.1 微积分的发展史
-
5.2 不定积分的概念
-
5.3 不定积分的基本公式与运算法则、直接积分法
-
5.4 第一类换元积分法
-
5.5 第二类换元积分法
-
5.6 分部积分法
-
6 定积分及其应用
-
6.1 定积分的概念
-
6.2 定积分的性质
-
6.3 积分上限函数及其导数
-
6.4 微积分基本公式
-
6.5 定积分的换元法
-
6.6 定积分的分部积分法
-
6.7 定积分的应用
-
6.7.1 定积分在几何上的应用
-
6.7.2 定积分在物理上的应用
-
7 线性代数初步
-
7.1 行列式
-
7.2 矩阵的概念
-
7.3 矩阵的运算
-
7.4 逆矩阵
-
7.5 矩阵的初等变换与秩
-
7.6 线性方程组
-
8 常微分方程
-
8.1 常微分方程的概念
-
8.2 一阶微分方程
-
8.2.1 可分离变量的微分方程
-
8.2.2 齐次微分方程
-
8.2.3 一阶线性微分方程
-
8.3 高阶线性微分方程
-
8.4 常系数齐次线性微分方程
-
9 数学实验
-
10 期末复习
-
1
目标及要求
-
2
学习视频
-
3
PPT
-
4
课堂测验
一、掌握基本积分公式:
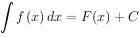
二、掌握不定积分的性质:
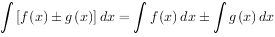
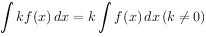
三、熟练运用直接积分法 :
简单函数直接求积分;
利用积分积分表求积分。

选择班级


